题目内容
我们学过二次函数的图象的平移,如:将二次函数y=3x2的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是y=3(x+2)2-4.类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
(1)将y=
| 1 |
| x |
(2)函数y=
| x+1 |
| x |
| 1 |
| x |
| x-1 |
| x-2 |
(3)一般地,函数y=
| x+b |
| x+a |
分析:(1)设新函数的解析式为y=
,原函数上的一个点为(1,1)向右平移1个单位后的点为(2,1)代入新函数得:k=-1,就有y=
再向上平移1个单位,点变为(2,2),设新函数为y=
+b,把新点代入得b=1那么y=
+1=
;
(2)先把所给函数进行分解得y=1+
,那么应是由y=
的图象向上平移1个单位得到;把后面的函数解析式分解得y=
+1,那么应是由y=
的图象先向右平移2个单位,再向上平移1个单位得到;
(3)由(1)(2)得到结论.
| 1 |
| x+k |
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x-1 |
| x |
| x-1 |
(2)先把所给函数进行分解得y=1+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x-2 |
| 1 |
| x |
(3)由(1)(2)得到结论.
解答:解:(1)y=
;y=
.(2分)
(2)上,1;(3分)
y=
可转化为y=
+1
它的图象可由反比例函数y=
的图象先向右平移2个单位,再向上平移1个单位得到.(4分)
(3)函数y=
(ab≠0,且a≠b)可转化为y=
+1.
当a>0时,y=
(ab≠0,且a≠b)的图象可由反比例函数y=
的图象
左平移a个单位,再向上平移一个单位得到;
当a<0时,y=
(ab≠0,且a≠b)的图象可由反比例函数y=
的图象向左平移-a个单位,再向上平移一个单位得到.(6分)
| 1 |
| x-1 |
| x |
| x-1 |
(2)上,1;(3分)
y=
| x-1 |
| x-2 |
| 1 |
| x-2 |
它的图象可由反比例函数y=
| 1 |
| x |
(3)函数y=
| x+b |
| x+a |
| b-a |
| x+a |
当a>0时,y=
| x+b |
| x+a |
| b-a |
| x |
左平移a个单位,再向上平移一个单位得到;
当a<0时,y=
| x+b |
| x+a |
| b-a |
| x |
点评:无论进行怎样的平移,反比例函数的弯曲度不会改变,即比例系数不变.左右平移改变点的横坐标;上下平移改变点的纵坐标.移动方法为:上加下减,左加右减.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 的图象沿y轴向上平移3个单位长度,得到函数 ______的图象,再沿x轴向右平移1个单位长度,得到函数 ______的图象;
的图象沿y轴向上平移3个单位长度,得到函数 ______的图象,再沿x轴向右平移1个单位长度,得到函数 ______的图象; 的图象可由哪个反比例函数的图象经过怎样的变换得到?
的图象可由哪个反比例函数的图象经过怎样的变换得到? 的图象沿y轴向上平移3个单位长度,得到函数 ______的图象,再沿x轴向右平移1个单位长度,得到函数 ______的图象;
的图象沿y轴向上平移3个单位长度,得到函数 ______的图象,再沿x轴向右平移1个单位长度,得到函数 ______的图象;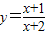 的图象可由哪个反比例函数的图象经过怎样的变换得到?
的图象可由哪个反比例函数的图象经过怎样的变换得到? 的图象沿y轴向上平移3个单位长度,得到函数 ______的图象,再沿x轴向右平移1个单位长度,得到函数 ______的图象;
的图象沿y轴向上平移3个单位长度,得到函数 ______的图象,再沿x轴向右平移1个单位长度,得到函数 ______的图象; 的图象可由哪个反比例函数的图象经过怎样的变换得到?
的图象可由哪个反比例函数的图象经过怎样的变换得到?