题目内容
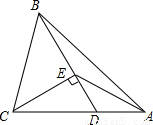
如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连结AE.
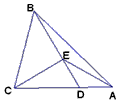
求证:(1)ED=DA;
(2)∠EBA=∠EAB ;
(3)BE2=AD·AC
(2)∠EBA=∠EAB ;
(3)BE2=AD·AC
证明:(1)∵CE⊥BD ∴∠CED=90°
又 ∠BDC=60°∴∠ECD=30°
∴CD=2ED ∵CD=2DA ∴ED=DA;
(2) ∵ED=DA ∴∠DEA=∠DAE
∵∠EDC=60° ∴∠EAD=∠DEA=30°
∵∠BAD=45° ∴∠EAB=15°
又∠BDC=∠DBA+∠BAD ∴∠DBA=15° ∴∠EAB=∠EBA;
(3)∵∠EAB=∠EBA
∴BE=AE
∵∠AED=∠ACE
∴△AED∽△ACE
∴ ∴AE2=AD·AC 即BE2=AD·AC
∴AE2=AD·AC 即BE2=AD·AC
又 ∠BDC=60°∴∠ECD=30°
∴CD=2ED ∵CD=2DA ∴ED=DA;
(2) ∵ED=DA ∴∠DEA=∠DAE
∵∠EDC=60° ∴∠EAD=∠DEA=30°
∵∠BAD=45° ∴∠EAB=15°
又∠BDC=∠DBA+∠BAD ∴∠DBA=15° ∴∠EAB=∠EBA;
(3)∵∠EAB=∠EBA
∴BE=AE
∵∠AED=∠ACE
∴△AED∽△ACE
∴
 ∴AE2=AD·AC 即BE2=AD·AC
∴AE2=AD·AC 即BE2=AD·AC
练习册系列答案
相关题目
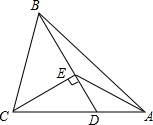 如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE. 25、
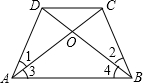
25、 证明题:(1)等腰梯形的对角线交点与同一底的两个端点的距离相等.
证明题:(1)等腰梯形的对角线交点与同一底的两个端点的距离相等.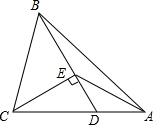 如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.