题目内容
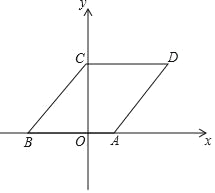
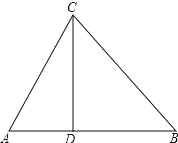
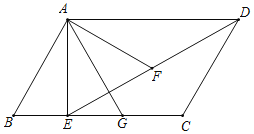
【题目】如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.
(1)求证:△AEF是等边三角形;
(2)若AB=2,求△AFD的面积.
【答案】(1)证明见解析;(2)S△ADF=![]() .
.
【解析】(1)先根据轴对称性质及BC∥AD证△ADE为直角三角形,由F是AD中点知AF=EF,再结合AE与AF关于AG对称知AE=AF,即可得证;
(2)由△AEF是等边三角形且AB与AG关于AE对称、AE与AF关于AG对称知∠EAG=30°,据此由AB=2知AE=AF=DF=![]() 、AH=
、AH=![]() ,从而得出答案.
,从而得出答案.
(1)∵AB与AG关于AE对称,
∴AE⊥BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE⊥AD,即∠DAE=90°,
∵点F是DE的中点,即AF是Rt△ADE的中线,
∴AF=EF=DF,
∵AE与AF关于AG对称,
∴AE=AF,
则AE=AF=EF,
∴△AEF是等边三角形;
(2)记AG、EF交点为H,
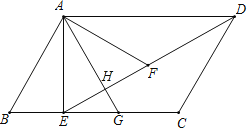
∵△AEF是等边三角形,且AE与AF关于AG对称,
∴∠EAG=30°,AG⊥EF,
∵AB与AG关于AE对称,
∴∠BAE=∠GAE=30°,∠AEB=90°,
∵AB=2,
∴BE=1、DF=AF=AE=![]() ,
,
则EH=![]() AE=
AE=![]() 、AH=
、AH=![]() ,
,
∴S△ADF=![]() ×
×![]() .
.

练习册系列答案
相关题目
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去……
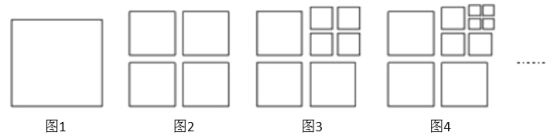
(1)根据图中的规律补全下表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
正方形个数 | 1 | 4 | 7 | 10 |
|
(2)求第几幅图形中有2020个正方形?