题目内容
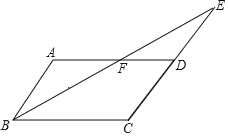
【题目】如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF,
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
【答案】①见解析②22
【解析】
①利用平行四边形的性质∠A=∠FDE,∠ABF=∠E,结合AF=DF,可判定△ABF≌△DEF,即可得出AB=DE;
②利用角平分线以及平行线的性质,即可得到AF=AB=3,进而得出BC=AD=6,CD=AB=3,依据△ABF≌△DEF,可得DE=AB=3,EF=BF=5,进而得到△BCE的周长.
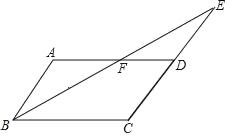
解:如图①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠A=∠FDE,∠ABF=∠E,
∵AF=DF,
∴△ABF≌△DEF,
∴AB=DE;
②∵BE平分∠ABC,
∴∠ABF=∠CBF,
∵AD∥BC,
∴∠CBF=∠AFB,
∴∠ABF=∠AFB,
∴AF=AB=3,
∴AD=2AF=6
∵四边形ABCD是平行四边形,
∴BC=AD=6,CD=AB=3,
∵△ABF≌△DEF,
∴DE=AB=3,EF=BF=5,
∴CE=6,BE=EF+BF=10,
∴△BCE的周长=BC+CE+BE=10+6+6=22.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】将一个正方体的表面涂上颜色.如图把正方体的棱![]() 等分,然后沿等分线把正方体切开,能够得到
等分,然后沿等分线把正方体切开,能够得到![]() 个小正方体,通过观察我们可以发现
个小正方体,通过观察我们可以发现![]() 个小正方体全是
个小正方体全是![]() 个面涂有颜色的.如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到
个面涂有颜色的.如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到![]() 个小正方体,通过观察我们可以发现这些小正方体中有
个小正方体,通过观察我们可以发现这些小正方体中有![]() 个是
个是![]() 个面涂有颜色的,有
个面涂有颜色的,有![]() 个是
个是![]() 个面涂有颜色的,有
个面涂有颜色的,有![]() 个是
个是![]() 个面涂有颜色的,还有
个面涂有颜色的,还有![]() 个各个面都没有涂色.
个各个面都没有涂色.

(1)如果把正方体的棱![]() 等分,所得小正方体表面涂色情况如何呢?把正方体的棱
等分,所得小正方体表面涂色情况如何呢?把正方体的棱![]() 等分呢?(请填写下表):
等分呢?(请填写下表):
棱等分数 |
|
|
| ___________个 | _____________个 |
| __________个 | ____________个 |
| ___________个 | ____________个 |
各个面都无涂色的正方体 | ___________个 | ____________个 |
(2)请直接写出将棱![]() 等分时只有一个面涂色的小正方体的个数_____________.
等分时只有一个面涂色的小正方体的个数_____________.