题目内容
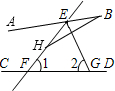 如图,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=50°,∠2=70°,则下列结论正确的是
如图,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=50°,∠2=70°,则下列结论正确的是
- A.∠FEG=60°
- B.∠BEG=70°
- C.线段EG是△EHB的角平分线
- D.AB∥CD
A
分析:已知∠1和∠2的度数,可以求出∠FEG=60°,所以∠BEG=60°,所以可以求出∠BEH=120°,进而可以判定AB与CD是否平行.
解答:A、若∠1=50°,∠2=70°,则根据内角和定理,∠FEG=180°-70°-50°=60°;故A正确.
B、因为EG平分∠BEF,所以∠BEG=∠FEG=60°;故B错误.
C、线段EG不是△EHB的角平分线,因为三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点和交点的线段叫三角形的角平分线;故C错误.
D、∠CEB=120°,∠1=70°,而∠CEB与∠1是同旁内角,但不互补,所以AB与CD不平行;故D错误.
故选A.
点评:本题结合角的比较与运算,考查了多个知识点,题目典型,难度不大.
分析:已知∠1和∠2的度数,可以求出∠FEG=60°,所以∠BEG=60°,所以可以求出∠BEH=120°,进而可以判定AB与CD是否平行.
解答:A、若∠1=50°,∠2=70°,则根据内角和定理,∠FEG=180°-70°-50°=60°;故A正确.
B、因为EG平分∠BEF,所以∠BEG=∠FEG=60°;故B错误.
C、线段EG不是△EHB的角平分线,因为三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点和交点的线段叫三角形的角平分线;故C错误.
D、∠CEB=120°,∠1=70°,而∠CEB与∠1是同旁内角,但不互补,所以AB与CD不平行;故D错误.
故选A.
点评:本题结合角的比较与运算,考查了多个知识点,题目典型,难度不大.

练习册系列答案
相关题目
 26、如图,直线EF分别交AB、AC于F、E交BC延长线于D,已知AB•BF=DB•BC.求证:AE•CE=DE•EF.
26、如图,直线EF分别交AB、AC于F、E交BC延长线于D,已知AB•BF=DB•BC.求证:AE•CE=DE•EF. 3、如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是( )
3、如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是( ) 5、如图,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=50°,∠2=70°,则下列结论正确的是( )
5、如图,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=50°,∠2=70°,则下列结论正确的是( ) 如图,直线EF分别交AB、CD于G、H.∠1=60°,∠2=120°,那么直线AB与CD的关系是
如图,直线EF分别交AB、CD于G、H.∠1=60°,∠2=120°,那么直线AB与CD的关系是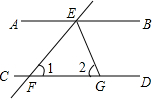 如图,直线EF分别交直线AB、CD于点E、F,EG平分∠BEF,若∠1=50°,∠2=65°,试判断直线AB与CD的位置关系,并说明理由.
如图,直线EF分别交直线AB、CD于点E、F,EG平分∠BEF,若∠1=50°,∠2=65°,试判断直线AB与CD的位置关系,并说明理由.