题目内容
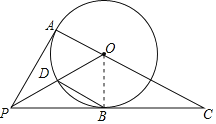
【题目】如图，PA，PB是⊙O的切线，A，B为切点．连接AO并延长交PB的延长线于点C，连接PO交⊙O于点D.
(1)求证：PO平分∠APC；
(2)连接BD，若∠C＝30°，求证：DB∥AC.
【答案】详见解析
【解析】
（1）连接OB，根据切线长定理即可解答；
（2）先证明△ODB是等边三角形，得到∠OBD=60°，再由∠DBP=∠C，即可得到DB∥AC．
（1）如图，连接OB，
∵PA，PB是⊙O的切线，
∴PO平分∠APC；
（2）∵OA⊥AP，OB⊥BP，
∴∠CAP=∠OBP=90°，
∵∠C=30°，
∴∠APC=90°-∠C=90°-30°=60°，
∵PO平分∠APC，
∴∠OPC=
∠APC=×60°=30°，
∴∠POB=90°-∠OPC=90°-30°=60°，
又OD=OB，
∴△ODB是等边三角形，
∴∠OBD=60°，
∴∠DBP=∠OBP-∠OBD=90°-60°=30°，
∴∠DBP=∠C，
∴DB∥AC．
练习册系列答案
相关题目
