题目内容
如图，已知CD是Rt△ABC斜边上的高，AD=3，BD=8则CD的长为（ ）分析：先证明∠ACD=∠CBD，从而可判定△ACD∽△CBD，继而根据相似三角形的对应边成比例可得出CD的长度．
解答：解：∵∠ACD+∠DCB=90°，∠CBD+∠DCB=90°，
∴∠ACD=∠CBD，
又∠ADC=∠CDB=90°，
∴△ACD∽△CBD，
∴
=
，即CD2=AD×DB=24，
∴CD=
=2
．
故选B．
∴∠ACD=∠CBD，
又∠ADC=∠CDB=90°，
∴△ACD∽△CBD，
∴
| AD |
| CD |
| CD |
| BD |
∴CD=
| 24 |
| 6 |
故选B．
点评：此题考查了相似三角形的判定与性质及直角三角形的性质，解答本题的关键是掌握相似三角形的判定定理，得出△ACD∽△CBD，难度一般．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
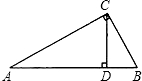如图，已知CD是Rt△ABC斜边上的高，AC=4，BC=3，计算cos∠BCD的值．
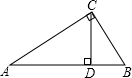如图，已知CD是Rt△ABC的斜边上的高，其中AD=9cm，BD=4cm，那么CD等于
如图，已知CD是Rt△ABC的斜边AB上的高，其中AD=6，BD=4，那么CD=
C.
24 D.
5 