题目内容
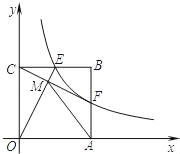
【题目】如图,平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,S△AEF=4,则下列结论:①FD=2AF;②S△BCE=36;③S△ABE=16; ④△AEF∽△ACD,其中一定正确的是( )

A.①②③④B.①②C.②③④D.①②③
【答案】B
【解析】
①根据四边形ABCD是平行四边形,可得OA=OC,AD∥BC,AD=BC,由点E是OA的中点,可得CE=3AE,再根据相似三角形对应边成比例即可判断;
②根据相似三角形的面积比等于相似比的平方即可判断;
③根据等高的两个三角形面积的比等于底边之比即可求出![]() 的面积;
的面积;
④假设△AEF∽△ACD,可得EF∥CD,即BF∥CD,由已知AB∥CD,可得BF和AB共线,由点E是OA的中点,即BE与AB不共线,得假设不成立,即![]() 和
和![]() 不相似,即可判断.
不相似,即可判断.
解:①∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,AD=BC,
∵点E是OA的中点,
∴CE=3AE,
∵AF∥BC,
∴△AEF∽△CEB,
∴![]() =
=![]() =3,
=3,
∴BC=3AF,
∴FD=2AF,
所以结论①正确;
②∵△AEF∽△CEB,CE=3AE,
∴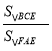 =32,
=32,
∴S△BCE=9S△FAE=36,
所以结论②正确;
③∵△ABE和△CBE等高,且CE=3AE,
∴S△BCE=3S△ABE,
∴S△ABE=12,
所以结论③错误;
④假设△AEF∽△ACD,
∴EF∥CD,即BF∥CD,
∵AB∥CD,
∴BF和AB共线,
∵点E是OA的中点,即BE与AB不共线,
∴假设不成立,即△AEF和△ACD不相似,
所以结论④错误.
综上所述:正确的结论有①②.
故选:B.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,从甲、乙两个大棚各收集了 24 株秧苗上的小西红柿的个数,并对数据进行整理、描述和分析。
下面给出了部分信息:(说明:45 个以下为产量不合格,45 个及以上为产量合格,其中 45~65 个为产量良好,65~85 个为产量优秀)
a.补全下面乙组数据的频数分布直方图(数据分成 6 组: 25≤x<35,35≤x<45,45≤x<55,55≤x<65,65≤x<75,75≤x<85):
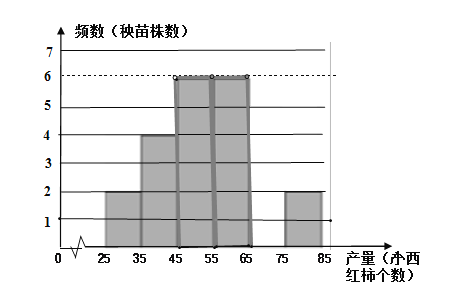
b.乙组数据在产量良好(45≤x<65)这两组的具体数据为: 46 46 47 47 48 48 55 57 57 57 58 61
c.数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 52.25 | 51 | 58 | 238 |
乙 | 52.25 | 57 | 210 |
(1)补全乙的频数分布直方图.
(2)写出表中![]() 的值.
的值.
(3)根据样本情况,估计乙大棚产量良好及以上的秧苗数为 株.
(4)根据抽样调查情况,可以推断出 大棚的小西红柿秧苗品种更适应市场需求,写出理由.(至少从两个不同的角度说明推断的合理性).
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?