题目内容
【题目】
(1)解方程: ![]() +
+ ![]() =2
=2
(2)如图,在⊙O中,OA⊥OB,∠A=20°,求∠B的度数.
【答案】
(1)解:去分母得,1﹣(x+2)=2(x﹣2),
去括号得,1﹣x﹣2=2x﹣4,
移项得,﹣x﹣2x=﹣4﹣1+2,
合并同类项得,﹣3x=﹣3,
系数化为1得,x=1,
经检验,x=1是原方程的解
(2)解:连接OC,
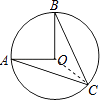
∵OA⊥OB,
∴∠AOB=90°,
∴∠ACB=45°.
又∴OA=OC,∠A=20°,
∴∠ACO=20°,
∴∠OCB=25°.
又∵OC=OB
∴∠B=25°.
【解析】(1)先把分式方程化为整式方程,求出x的值,再代入最简公分母进行检验即可;(2)连接OC,先根据圆周角定理求出∠ACB的度数,再由等腰三角形的性质求出∠ACO的度数,进而可得出∠BCO的度数,据此可得出结论.
【考点精析】通过灵活运用去分母法和圆周角定理,掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.

练习册系列答案
相关题目