题目内容
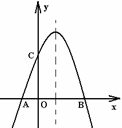
如图,抛物线的对称轴是直线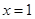 ,它与
,它与 轴交于
轴交于 ,
, 两点,与
两点,与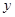 轴交于
轴交于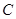 点,点
点,点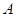 ,
,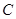 的坐标分别是
的坐标分别是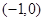 ,
,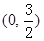 .
.
(1) 求此抛物线对应的函数解析式;
(2) 若点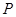 是抛物线上位于
是抛物线上位于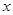 轴上方的一个动点,求△ABP面积的最大值.
轴上方的一个动点,求△ABP面积的最大值.
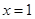 ,它与
,它与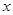 轴交于
轴交于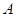 ,
,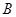 两点,与
两点,与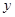 轴交于
轴交于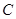 点,点
点,点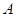 ,
,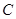 的坐标分别是
的坐标分别是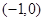 ,
,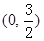 .
.
(1) 求此抛物线对应的函数解析式;
(2) 若点
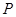 是抛物线上位于
是抛物线上位于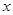 轴上方的一个动点,求△ABP面积的最大值.
轴上方的一个动点,求△ABP面积的最大值.(1)y=-x2+2x+3;(2)8
试题分析:(1)已知对称轴是直线
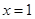 ,故可设顶点式,再根据图象过点
,故可设顶点式,再根据图象过点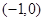 ,
,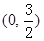 ,即可根据待定系数法求得函数关系式;
,即可根据待定系数法求得函数关系式;(2)△ABP中可把AB看作底,P点的纵坐标作为高,当△ABP面积的最大时,即点P的纵坐标最大,此时点P为二次函数的顶点坐标,从而可以求得结果.
(1) ∵抛物线的对称轴是直线x=1,
设抛物线的解析式是y=a(x-1)2+k
∵图象过点
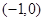 ,
,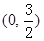 .
.∴0=4a+k
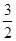 =a+k
=a+k解得:a=-1,k="4"
∴y=-(x-1)2+4即y=-x2+2x+3 ;
(2)当x=1时,P点的纵坐标值最大y=4,x轴上两个交点分别是A(-1,0)B(3,0)
此时三角形ABP的面积最大S=4
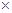 4
4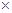
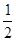 =8.
=8.点评:解答本题的关键是注意当二次函数的问题中明确了对称轴时,一般应设顶点式,同时熟练掌握二次函数的顶点坐标.

练习册系列答案
相关题目
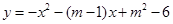 交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.
交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.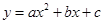 的图像经过
的图像经过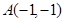 、
、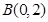 、
、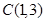 ;
;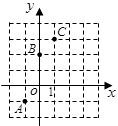
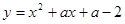 .
.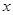 轴相交于A(
轴相交于A(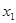 ,0),B(
,0),B(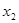 ,0),且
,0),且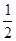 ;④b<1.其中正确的结论是( )
;④b<1.其中正确的结论是( )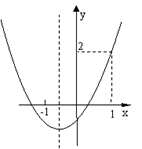
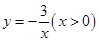 ,②
,②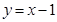 ,③
,③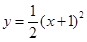 ,④
,④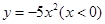 中,
中,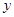 随
随 的增大而增大的函数有( )
的增大而增大的函数有( )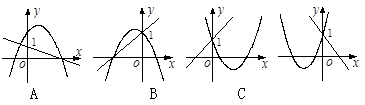
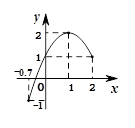
 的图象如图所示.当
的图象如图所示.当 <0时,自变量
<0时,自变量 的取值范围是(
的取值范围是( 
 <3
<3