题目内容
【题目】等腰Rt△ABC中,CA=CB,∠ACB=90°,点O是AB的中点.
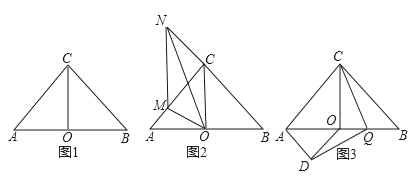
(1)如图1,求证:CO=BO;
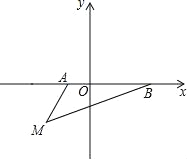
(2)如图2,点M在边AC上,点N在边BC延长线上,MN﹣AM=CN,求∠MON的度数;
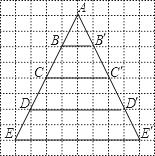
(3)如图3,AD∥BC,OD∥AC,AD与OD交于点D,Q是OB的中点,连接CQ、DQ,试判断线段CQ与DQ的关系,并给出证明.
【答案】(1)详见解析;(2)45°;(3)QC=QD,QC⊥QD,理由详见解析.
【解析】
(1)根据等腰三角形的三线合一证明;
(2)在线段BC上取点H,使CH=AM,连接OH,分别证明△AOM≌△COH和△MON≌△HON,根据全等三角形的性质计算即可;
(3)作DG⊥AO于G,证明△COQ≌△QGD,根据全等三角形的性质,垂直的定义证明.
(1)∵∠ACB=90°,AO=BO,
∴CO=![]() AB=BO;
AB=BO;
(2)在线段BC上取点H,使CH=AM,连接OH,如图所示
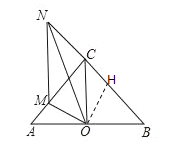
∵∠ACB=90°,AO=BO,
∴∠A=∠B=45°,∠ACO=∠BCO=45°,
在△AOM和△COH中,
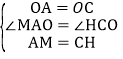 ,
,
∴△AOM≌△COH(SAS)
∴OM=OH,
∵MN﹣AM=CN,
∴NM=NH,
在△MON和△HON中,
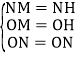 ,
,
∴△MON≌△HON(SSS),
∴∠MON=∠HON,
∴∠MON=∠AOM+∠CON,
∴∠MON=![]() ∠AOC=45°;
∠AOC=45°;
(3)QC=QD,QC⊥QD,
理由如下:作DG⊥AO于G,
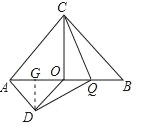
∵AD∥BC,
∴∠OAD=∠B=45°,
∵OD∥AC,
∴∠AOD=∠OAC=45°,
∴DA=DO,又DG⊥AO,
∴DG=AG=GO=![]() OA,
OA,
∵Q是OB的中点,
∴OQ=BQ=![]() OB,
OB,
∴DG=OQ,GQ=OC,
在△COQ和△QGD中,
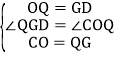 ,
,
∴△COQ≌△QGD(SAS),
∴QC=QD,∠GQD=∠OCQ,
∵∠OCQ+∠CQO=90°,
∴∠GQD+∠CQO=90°,即∠CQD=90°,
∴QC⊥QD,
则QC=QD,QC⊥QD.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案