题目内容
(1)如图,已知AC平分∠BAD,∠1=∠2,求证:AB=AD.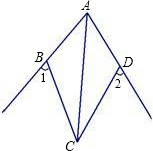

(2)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
①求∠EBC的度数;
②求证:BD=CD.
分析:(1)首先依题意证明△ABC≌△ADC继而求得AB=AD.
(2)①∠EBC的度数等于∠ABC-∠ABE,因而求∠EBC的度数就可以转化为求∠ABC和∠ABE,根据等腰三角形的性质等边对等角,就可以求出.
②在等腰三角形ABC中,根据三线合一定理即可证得.
(2)①∠EBC的度数等于∠ABC-∠ABE,因而求∠EBC的度数就可以转化为求∠ABC和∠ABE,根据等腰三角形的性质等边对等角,就可以求出.
②在等腰三角形ABC中,根据三线合一定理即可证得.
解答:(1)证明:∵AC平分∠BAD,
∴∠BAC=∠DAC.
∵∠1=∠2,
∴∠ABC=∠ADC.
在△ABC和△ADC中,
∵
,
∴△ABC≌△ADC(AAS).
∴AB=AD;
(2)解:①∵AB是⊙O的直径,
∴∠AEB=90°.
又∵∠BAC=45°,
∴∠ABE=45°.
又∵AB=AC,
∴∠ABC=∠C=67.5°.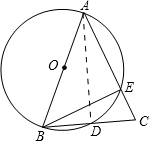
∴∠EBC=22.5°.
②证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
又∵AB=AC,
∴BD=CD.
∴∠BAC=∠DAC.
∵∠1=∠2,
∴∠ABC=∠ADC.
在△ABC和△ADC中,
∵
|
∴△ABC≌△ADC(AAS).
∴AB=AD;
(2)解:①∵AB是⊙O的直径,
∴∠AEB=90°.
又∵∠BAC=45°,
∴∠ABE=45°.
又∵AB=AC,
∴∠ABC=∠C=67.5°.

∴∠EBC=22.5°.
②证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
又∵AB=AC,
∴BD=CD.
点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等.同时也考查圆周角定理及等腰三角形的性质的综合运用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 19、如图,已知AC与BD相交于点E,DE=CE,AE=BE.求证:∠A=∠B.
19、如图,已知AC与BD相交于点E,DE=CE,AE=BE.求证:∠A=∠B.
 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD. 如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等( )
如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等( ) 如图,已知AC=DB,若要依据“SAS”判定△ABC≌△DCB,还应添加的一个条件是
如图,已知AC=DB,若要依据“SAS”判定△ABC≌△DCB,还应添加的一个条件是