题目内容
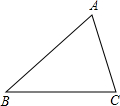 如图,在一块三角形的地块中间建一个圆形花坛,要使它与三边都相切.
如图,在一块三角形的地块中间建一个圆形花坛,要使它与三边都相切.(1)用尺规作图法画出这个圆 (保留作图痕迹,不写作法);
(2)设三角形的面积为S,周长为L,内切圆半径为r,则S=
| 1 | 2 |
分析:(1)由于所作圆与三角形三边都相切,所以是三角形的内切圆,圆心在三角形的三个内角的平分线交点处,由此即可求解;
(2)设圆心为0,切点分别为D,E,F.连接AO,BO.CO,DO,EO,FO,然后利用三角形的面积公式即可求解.
(2)设圆心为0,切点分别为D,E,F.连接AO,BO.CO,DO,EO,FO,然后利用三角形的面积公式即可求解.
解答: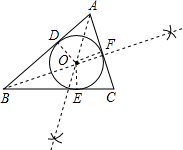 解:(1)如图,⊙O就是所求的圆;
解:(1)如图,⊙O就是所求的圆;
(2)设圆心为0,切点分别为D,E,F,
连接AO,BO.CO,DO,EO,FO,
S=
AB×r+
BC×r+
AC×r,
=
r(AB+BC+AC),
=
Lr.
 解:(1)如图,⊙O就是所求的圆;
解:(1)如图,⊙O就是所求的圆;(2)设圆心为0,切点分别为D,E,F,
连接AO,BO.CO,DO,EO,FO,
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:此题主要考查了三角形的内切圆与内心的性质,作图的时候根据内切圆的圆心在实际行动的内角角平分线交点的性质即可解决问题;第二问利用面积的割补法即可解决问题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
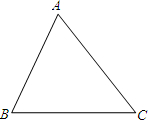 如图,在一块三角形的铁皮上裁出一个半圆形,需要先在铁皮上画出一个半圆,使得圆心在线段AC上,且与AB、BC相切.
如图,在一块三角形的铁皮上裁出一个半圆形,需要先在铁皮上画出一个半圆,使得圆心在线段AC上,且与AB、BC相切.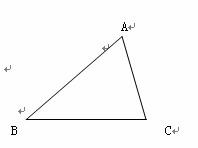
 Lr,请说明理由.
Lr,请说明理由.