题目内容
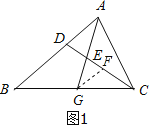
【题目】如图1,在△ABC中,G是BC的中点,E是AG的中点,CE的延长线交AB于D,求AD:BD

(1)解:过G作GF∥AB,交CD于F.
请继续完成解答过程:
(2)创新求解:利用“杠杆平衡原理”
解答本题:(如图2)设G点为杠杆BC的支点,B端所挂物体质量为1Kg;则C端所挂物体质量为1Kg,G点承受质量为2Kg;当E点为杠杆AG的支点,则A端所挂物体质量为2Kg;
再以D为杠杆AB的支点时,AD:BD=1kg:2kg=1:2应用:如图3,在△ABC中,G是BC上一点,E是AG上一点,CE的延长线交AB于D,且![]() =
=![]() ,
,![]() =2,求AD:BD
=2,求AD:BD
解:设G点为杠杆BC的支点,B端所挂物体质量为6Kg,则C端所挂物体质量为 kg,G点承受质量为 kg;当E点为杠杆AG的支点,则A端所挂物体质量为 kg;再以D为杠杆AB的支点时,AD:BD= .
【答案】(1)AD:BD=1:2;(2)4,10,5,6:5.
【解析】
试题分析:(1)如图1,过G作GF∥AB,交CD于F,得到△EFG∽△ADE,根据相似三角形的想知道的![]() ,求得GF=AD,根据△CGF∽△CBD,得到
,求得GF=AD,根据△CGF∽△CBD,得到![]() ,即可得到结论;
,即可得到结论;
(2)根据题目中提供的解题思路和方法,结合(1)的结论即可得到答案.
解:(1)如图1,过G作GF∥AB,交CD于F,
∴△EFG∽△ADE,
∴![]() ,
,
∵E是AG的中点,
∴![]() =1,
=1,
∴GF=AD,
∵GF∥BD,
∴△CGF∽△CBD,
∴![]() ,
,
∵G是BC的中点,
∴![]() ,
,
∴AD:BD=1:2;
(2)设G点为杠杆BC的支点,B端所挂物体质量为6Kg,
∵![]() =
=![]() ,
,
∴C端所挂物体质量:B端所挂物体质量=![]() =
=![]() ,
,
∴C端所挂物体质量=4kg,G点承受质量=C端所挂物体质量+B端所挂物体质量=10kg;
当E点为杠杆AG的支点,
∵![]() =2,
=2,
∴A端所挂物体质量:G点承受质量=1:2,
∴A端所挂物体质量=5kg;
以D为杠杆AB的支点时,AD:BD=B端所挂物体质量:A端所挂物体质量=6:5.
故答案为:4,10,5,6:5.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案