题目内容
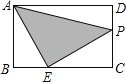
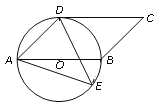
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
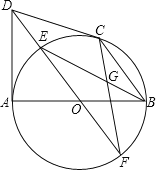
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
【答案】解:(1)证明:连接OC,
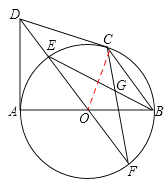
∵DC是⊙O切线,∴OC⊥DC。
∵OA⊥DA,∴∠DAO=∠DCO=90°。
在Rt△DAO和Rt△DCO中,
∵DO=DO,OA=OC,
∴Rt△DAO≌Rt△DCO(HL)。
∴DA=DC.
(2)连接BF、CE、AC,设AC与OD相交于点M,
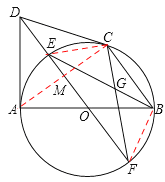
由切线长定理得:DC=DA=4,DO⊥AC,
∴DO平分AC。
在Rt△DAO中,AO=3,AD=4,
由勾股定理得:DO=5。
∵由三角形面积公式得:![]() DAAO=
DAAO=![]() DOAM,
DOAM,
则AM=![]() 。
。
同理CM=AM=![]() 。∴AC=
。∴AC=![]() 。
。
∵AB是直径,∴∠ACB=90°。
由勾股定理得:![]() 。
。
∵由圆周角定理得∠GCB=∠GEF,∠GFE=∠GBC,∴△BGC∽△EGF。
∴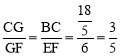 。
。
在Rt△OMC中,CM=![]() ,OC=3,由勾股定理得:OM=
,OC=3,由勾股定理得:OM=![]() 。
。
在Rt△EMC中,CM=![]() ,ME=OE﹣OM=3﹣
,ME=OE﹣OM=3﹣![]() =
=![]() ,由勾股定理得:CE=
,由勾股定理得:CE=![]() 。
。
在Rt△CEF中,EF=6,CE=![]() ,由勾股定理得:CF=
,由勾股定理得:CF=![]() 。
。
∵CF=CG+GF,![]() ,∴CG=
,∴CG=![]() CF=
CF=![]() ×
×![]() =
=![]() 。
。
【解析】
试题分析:(1)连接OC,∠DAO=∠DCO=90°,根据HL证Rt△DAO≌Rt△DCO,根据全等三角形的性质推出即可。
(2)连接BF、CE、AC,由切线长定理求出DC=DA=4,求出DO=5,CM、AM的长,由勾股定理求出BC长,根据△BGC∽△EGF求出![]() ,则CG=
,则CG=![]() CF;利用勾股定理求出CF的长,则CG的长度可求得。
CF;利用勾股定理求出CF的长,则CG的长度可求得。

练习册系列答案
相关题目