题目内容
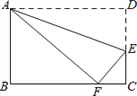
【题目】如图,在矩形ABCD中AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么![]() 的值是_________.
的值是_________.
【答案】![]()
【解析】分析: 根据翻转变换的性质得到∠AFE=∠D=90°,AF=AD=5,根据矩形的性质得到∠EFC=∠BAF,根据余弦的概念计算即可.
详解: 由翻转变换的性质可知,∠AFE=∠D=90°,AF=AD=5,
∴∠EFC+∠AFB=90°,
∵∠B=90°,
∴∠BAF+∠AFB=90°,
∴∠EFC=∠BAF,
cos∠BAF=![]() =
=![]() ,
,
∴cos∠EFC=![]() ,
,
故答案为:![]() .
.
点睛: 本题考查的是翻折变换的性质、余弦的概念,掌握翻折变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
相关题目