题目内容
【题目】如果等腰三角形一腰上的高与另一腰的夹角45°，那么这个等腰三角形的底角为（ ）
A. 67°50′B. 22°C. 67.5°D. 22.5°或67.5°
【答案】D
【解析】
先知三角形有两种情况（1）（2），求出每种情况的顶角的度数，再利用等边对等角的性质（两底角相等）和三角形的内角和定理，即可求出底角的度数．
有两种情况；
（1）如图当△ABC是锐角三角形时，BD⊥AC于D，
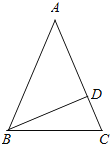
则∠ADB=90°，
已知∠ABD=45°，
∴∠A=90°-45°=45°，
∵AB=AC，
∴∠ABC=∠C=
×（180°-45°）=67.5°；
（2）如图，当△EFG是钝角三角形时，FH⊥EG于H，
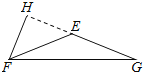
则∠FHE=90°，
已知∠HFE=45°，
∴∠HEF=90°-45°=45°，
∴∠FEG=180°-45°=135°，
∵EF=EG，
∴∠EFG=∠G=×（180°-135°）=22.5°，
综合（1）（2）得：等腰三角形的底角是67.5°或22.5°，
故选D．
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数
与方差s2如下表所示：
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（ ）
A. 甲B. 乙C. 丙D. 丁
【题目】在一组数据x1,x2,…,xn中,各数据与它们的平均数
的差的绝对值的平均数,即T=
(|x1-|+|x2-|+…+|xn-|)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度.“平均差”越大说明数据的离散程度越大.因为“平均差”的计算比方差的计算要容易一点,所以有时人们也用它代替方差来比较数据的离散程度.最大值与最小值的差、方差(标准差)、平均差都是反映数据离散程度的量.
一水产养殖户李大爷要了解鱼塘中鱼的质量的离散程度,因为个头大小差异太大会出现“大鱼吃小鱼”的情况.为防止出现“大鱼吃小鱼”的情况,在能反映数据离散程度的几个量中某些值超标时就要捕捞,分开养殖或出售.他从甲、乙两个鱼塘各随机捕捞10条鱼称得质量(单位:千克)如下:
甲鱼塘:3、5、5、5、7、7、5、5、5、3
乙鱼塘:4、4、5、6、6、5、6、6、4、4
(1)分别计算从甲、乙两个鱼塘中抽取的10条鱼的质量的极差(极差:最大值与最小值的差)、方差、平均差.完成下面的表格:
极差(千克) | 方差 | 平均差(千克) | |
甲鱼塘 | |||
乙鱼塘 |
(2)如果你是技术人员,你会告诉李大爷哪个鱼塘的风险更大些?哪些量更能说明鱼质量的离散程度?
