题目内容
 印度数学家拜斯迦罗(公元1114~1185年)的著作中有个有趣的“荷花问题”:
印度数学家拜斯迦罗(公元1114~1185年)的著作中有个有趣的“荷花问题”:湖静浪平六月天,荷花半尺出水面;
忽来一阵狂风急,吹倒花儿水中偃.
湖面之上不复见,入秋渔翁始发现;
残花离根二尺遥,试问水深尺若干?
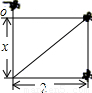
即:如图,在平静的湖面上,有一朵荷花高出水面半尺,忽然一阵狂风把荷花吹倒在水中淹没了.到了秋天,渔翁发现,淹没在水中的残花离根部有二尺远,试问水深是多少尺?答:
3.75
3.75
尺.分析:根据题意可设水深x尺,则荷花茎的长度为(x+0.5)尺,根据勾股定理可得:(x+0.5)2=x2+22,再解方程即可.
解答:解:设水深x尺,则荷花茎的长度为(x+0.5)尺,
根据勾股定理得:(x+0.5)2=x2+22,
解得:x=3.75,
故答案为:3.75.
根据勾股定理得:(x+0.5)2=x2+22,
解得:x=3.75,
故答案为:3.75.
点评:此题主要考查了勾股定理的应用,关键是根据题意表示出水深和荷花茎的长度.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 26、“印度荷花问题”
26、“印度荷花问题”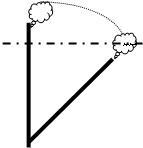 “印度荷花问题”
“印度荷花问题”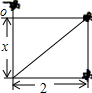 印度数学家拜斯迦罗(公元1114~1185年)的著作中有个有趣的“荷花问题”:
印度数学家拜斯迦罗(公元1114~1185年)的著作中有个有趣的“荷花问题”: