题目内容
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
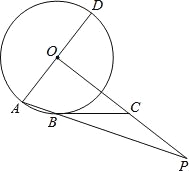
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
【答案】(1)证明见解析(2)7
【解析】
试题分析:(1)连结OB.由等腰三角形的性质得到∠A=∠OBA,∠P=∠CBP,由于OP⊥AD,得到∠A+∠P=90°,于是得到∠OBA+∠CBP=90°,求得∠OBC=90°结论可得;
(2)连结DB.由AD是⊙O的直径,得到∠ABD=90°,推出Rt△ABD∽Rt△AOP,得到比例式![]() ,即可得到结果.
,即可得到结果.
试题解析:(1)连结OB.
∵OA=OB,∴∠A=∠OBA,
又∵BC=PC,
∴∠P=∠CBP,
∵OP⊥AD,
∴∠A+∠P=90°,
∴∠OBA+∠CBP=90°,
∴∠OBC=180°﹣(∠OBA+∠CBP)=90°,
∵点B在⊙O上,
∴直线BC是⊙O的切线,
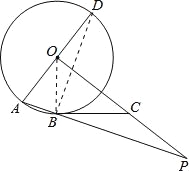
(2)如图,连结DB.
∵AD是⊙O的直径,
∴∠ABD=90°,
∴Rt△ABD∽Rt△AOP,
∴![]() ,即
,即![]() ,AP=9,
,AP=9,
∴BP=AP﹣BA=9﹣2=7.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目