题目内容

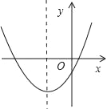
【题目】二次函数y=mx2+（6﹣2m）x+m﹣3的图象如图所示，则m的取值范围是（　　）

A. m＞3 B. m＜3 C. 0≤m≤3 D. 0＜m＜3

【答案】D

【解析】

由抛物线的开口向上知m＞0，由对称轴在y轴的左侧可与得到x=﹣＜0，由二次函数与y轴交于负半轴可以推出m﹣3＜0，又抛物线与x轴有两个交点（b2﹣4ac＞0），可以得到（6﹣2m）2﹣4m（m﹣3）＞0，然后利用前面的结论即可确定m的取值范围．

∵抛物线的开口向上，∴m＞0，①

∵对称轴在y轴的左侧，∴x=﹣＜0，②

∵二次函数与y轴交于负半轴，∴m﹣3＜0，③

∵抛物线与x轴有两个交点（b2﹣4ac＞0），∴（6﹣2m）2﹣4m（m﹣3）＞0，④

联立①②③④解得：0＜m＜3，∴m的取值范围是0＜m＜3．

故选D．

练习册系列答案
相关题目

【题目】在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数y(次/分)是这个人年龄x(岁)的一次函数。

(1)根据图中信息，求在正常情况下，y关于x的函数关系式；

(2)若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问：他是否有危险?为什么?

【题目】如图，已知抛物线y=x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P时直线AC下方抛物线上的动点．

（1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；

（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

【题目】如图是某旅游景点的一处台阶，其中台阶坡面AB和BC的长均为6m，AB部分的坡角∠BAD为45°，BC部分的坡角∠CBE为30°，其中BD⊥AD，CE⊥BE，垂足为D，E．现在要将此台阶改造为直接从A至C的台阶，如果改造后每层台阶的高为22cm，那么改造后的台阶有多少层？（最后一个台阶的高超过15cm且不足22cm时，按一个台阶计算．可能用到的数据：≈1.414，≈1.732）

【题目】综合与探究

如图，抛物线y=﹣与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，直线l经过B，C两点，点M从点A出发以每秒1个单位长度的速度向终点B运动，连接CM，将线段MC绕点M顺时针旋转90°得到线段MD，连接CD，BD．设点M运动的时间为t（t＞0），请解答下列问题：

（1）求点A的坐标与直线l的表达式；

（2）①直接写出点D的坐标（用含t的式子表示），并求点D落在直线l上时的t的值；

②求点M运动的过程中线段CD长度的最小值；

（3）在点M运动的过程中，在直线l上是否存在点P，使得△BDP是等边三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

【题目】综合与实践

（1）问题发现

如图1，和均为等边三角形，点在同一直线上，连接．请写出的度数及线段之间的数量关系，并说明理由．

（2）类比探究

如图2，和均为等腰直角三角形，，点在同一直线上，为中边上的高，连接．

填空：①的度数为____________；

②线段之间的数量关系为_______________________________．

（3）拓展延伸

在（2）的条件下，若，则四边形的面积为______________．

【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．

（1）求证：ED为⊙O的切线；

（2）如果⊙O的半径为，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．

【答案】（1）证明见解析；（2）

【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得≌ 即可得，则可证得为的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得 利用勾股定理即可求得的长，又由OE∥AB，证得根据相似三角形的对应边成比例，即可求得的长，然后利用三角函数的知识，求得与的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．

试题解析：(1)证明：连接OD，

∵OE∥AB，

∴∠COE=∠CAD，∠EOD=∠ODA，

∵OA=OD,

∴∠OAD=∠ODA，

∴∠COE=∠DOE，

在△COE和△DOE中，

∴△COE≌△DOE(SAS)，

∴ED⊥OD，

∴ED是的切线；

(2)连接CD，交OE于M，

在Rt△ODE中，

∵OD=32，DE=2，

∵OE∥AB，

∴△COE∽△CAB，

∴AB=5，

∵AC是直径，

∵EF∥AB，

∴S△ADF=S梯形ABEFS梯形DBEF

∴△ADF的面积为

【题型】解答题
【结束】
25

【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．

（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；

（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

【题目】我们知道，有一个内角是直角的三角形是直角三角形，其中直角所在的两条边叫直角边，直角所对的边叫斜边（如图①所示）．数学家还发现：在一个直角三角形中，两条直角边长的平方和等于斜边长的平方。即如果一个直角三角形的两条直角边长度分别是和，斜边长度是，那么。

（1）直接填空：如图①，若a＝3，b＝4，则c＝ ；若，，则直角三角形的面积是 ______ 。

（2）观察图②，其中两个相同的直角三角形边AE、EB在一条直线上，请利用几何图形的之间的面积关系，试说明。

（3）如图③所示，折叠长方形ABCD的一边AD，使点D落在BC边的点F处，已知AB＝8，BC＝10，利用上面的结论求EF的长？

【题目】如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=2，DE=1，BD=8，设CD=x．

（1）用含x的代数式表示AC+CE的长；

（2）请问点C满足什么条件时，AC+CE的值最小；

（3）根据（2）中的规律和结论，请构图求出代数式的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网