题目内容
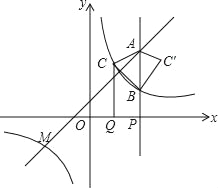
【题目】如图,直线![]() 和
和![]() 相交于点C,分别交x轴于点A和点B点P为射线BC上的一点。
相交于点C,分别交x轴于点A和点B点P为射线BC上的一点。
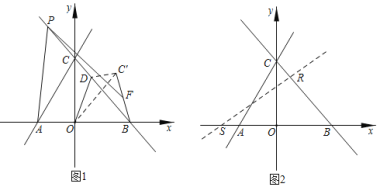
(1)如图1,点D是直线CB上一动点,连接OD,将![]() 沿OD翻折,点C的对应点为
沿OD翻折,点C的对应点为![]() ,连接
,连接![]() ,并取
,并取![]() 的中点F,连接PF,当四边形AOCP的面积等于
的中点F,连接PF,当四边形AOCP的面积等于![]() 时,求PF的最大值;
时,求PF的最大值;
(2)如图2,将直线AC绕点O顺时针方向旋转α度![]() ,分别与x轴和直线BC相交于点S和点R,当
,分别与x轴和直线BC相交于点S和点R,当![]() 是等腰三角形时,直接写出α的度数.
是等腰三角形时,直接写出α的度数.
【答案】(1)PF的最大值是![]() ;(2)
;(2)![]() 的度数:
的度数:![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)设P(m,-m+6),连接OP.根据S四边形AOCP=S△AOP+S△OCP=![]() ,构建方程求出点P坐标,取OB的中点Q,连接QF,QP,求出FQ,PQ,根据PF≤PQ+QF求解即可.
,构建方程求出点P坐标,取OB的中点Q,连接QF,QP,求出FQ,PQ,根据PF≤PQ+QF求解即可.
(2)分四种情形:①如图2-1中,当RS=RB时,作OM⊥AC于M.②如图2-2中,当BS=BR时,③如图2-3中,当SR=SB时,④如图2-4中,当BR=BS时,分别求解即可解决问题.
解:(1)在![]() 中,当
中,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ﹒
﹒
∴![]() ,
,![]()
设![]() ,连接OP
,连接OP
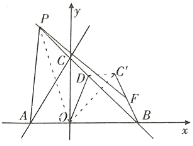
∴![]()
∴![]()
∴![]() ∴
∴![]()
取OB的中点Q,连接FQ,PQ
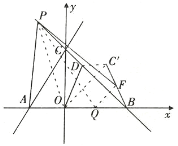
在![]() 中,当
中,当![]() 时,
时,![]()
∴![]() ∴
∴![]()
又∵点F是![]() 的中点,
的中点,
∴![]()
∵![]()
所以PF的最大值是![]()
(2)①如图2-1中,当RS=RB时,作OM⊥AC于M.
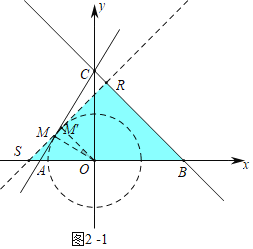
∵tan∠OAC=![]() =
=![]() ,
,
∴∠OAC=60°,
∵OC=OB=6,
∴∠OBC=∠OCB=45°,
∵∠OM′S=∠BRS=90°,
∴OM′∥BR,
∴∠AOM′=∠OBC=45°,
∵∠AOM=30°,
∴α=45°-30°=15°.
②如图2-2中,当BS=BR时,易知∠BSR=22.5°,
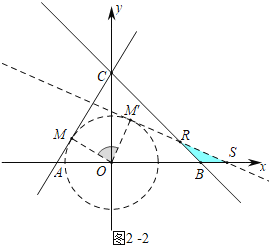
∴∠SOM′=90°-22.5°=67.5°,
∴α=∠MOM′=180°-30°-67.5°=82.5°
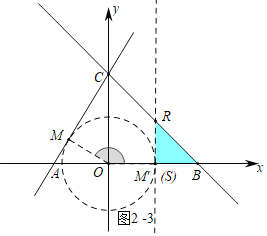
③如图2-3中,当SR=SB时,α=180°-30°=150°.
④如图2-4中,当BR=BS时,α=150°+(90°-67.5°)=172.5°.
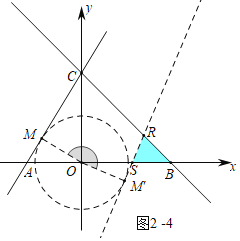
综上所述,满足条件的α的值为15°或82.5°或150°或172.5°.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】八年级(1)班张山同学利用所学函数知识,对函数![]() 进行了如下研究:
进行了如下研究:
列表如下:
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |
描点并连线(如下图)
(1)自变量x的取值范围是________;
(2)表格中:![]() ________,
________,![]() ________;
________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______.
的图象交点的坐标为_______.