题目内容
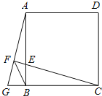
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,则
,则![]() 的长为________.
的长为________.
【答案】.![]()
【解析】
作FM⊥GC于M,则FM∥AB,由正方形的性质得出∠ABC=90°,AB=CB=6,由ASA证明△ABG≌△CBE,得出BG=BE,AG=CE,由AE=2BE,得出BG=BE=2,由勾股定理求出AGCE=AG=2![]() ,证明△AFE∽△CBE,得出对应边成比例求出AF=
,证明△AFE∽△CBE,得出对应边成比例求出AF=![]() ,求出FG=AGAF=
,求出FG=AGAF=![]() ,由平行线得出
,由平行线得出![]() ,求出FM=
,求出FM=![]() ,GM=
,GM=![]() ,得出BM=BGGM=
,得出BM=BGGM=![]() ,再由勾股定理求出BF即可.
,再由勾股定理求出BF即可.
作FM⊥GC于M,如图所示:

则FM∥AB,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=CB=6,
∴∠ABG=90°,
∴∠G+∠BAG=90°,
∵CF⊥AG,
∴∠AFE=∠CFG=90°,
∴∠G+∠BCE=90°,
∴∠BAG=∠BCE,
在△ABG和△CBE中,
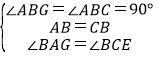 ,
,
∴△ABG≌△CBE(ASA),
∴BG=BE,AG=CE,
∵AE=2BE,
∴BE=2,AE=4,
∴BG=BE=2,∴CE=AG=![]() ,
,
∵∠AFE=∠ABC=90°,∠BAG=∠BCE,
∴△AFE∽△CBE,
∴![]() ,即
,即![]() ,
,
解得:AF=![]() ,
,
∴FG=AGAF=![]() ,
,
∵FM∥AB,
∴![]() ,
,
即![]() ,
,
解得:FM=![]() ,GM=
,GM=![]() ,
,
∴BM=BGGM=![]() ,
,
∴BF=![]() ;
;
故答案为:![]()

【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
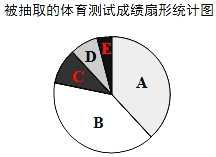
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.