题目内容
【题目】在矩形ABCD中 ,AB=4,BC=3,点P在边AB上.若将△DAP沿DP折叠 ,使点A落在矩形ABCD的对角线上,则AP的长为____.

【答案】![]() 或
或![]()
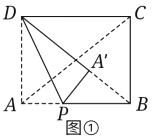
【解析】试题分析:如图①所示,当A′落在对角线BD上时,设AP的长度为x,则AP=A′P=x,PB=4-x,在△ABD和△A′BP中,因为∠A′BP=∠ABD,∠BA′P=∠BAD=90°,所以△ABD∽△A′BP,根据相似三角形的性质可得![]() ,在Rt△ABD中,BD=
,在Rt△ABD中,BD=![]() =5,则可得
=5,则可得![]() ,解得x=
,解得x=![]() ;
;
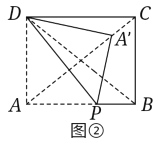
如图②所示,当A′落在对角线AC上时,根据折叠的性质,可得DP⊥AC,设AP=x,在△DAP和△ABC中,因为∠ADP+∠APD=90°,∠BAC+∠APD=90°,可得∠BAC=∠ADP,又因为∠BAC=∠ABC,所以△DAP∽△ABC,根据相似三角形的性质可得![]() ,即
,即![]() ,解得x=
,解得x=![]() .
.
故答案为: ![]() 或
或![]() .
.

练习册系列答案
相关题目