题目内容
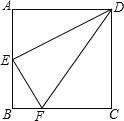
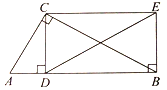
【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D ，BE⊥AB，垂足为B，BE=CD连接CE，DE.
（1）求证：四边形CDBE是矩形
（2）若AC=2 ，∠ABC=30°，求DE的长
【答案】（1）见详解,（2）DE =2
【解析】
（1）利用有一组对边平行且相等的四边形是平行四边形,有一个角是90°的平行四边形是矩形即可证明,（2）利用30°角所对直角边是斜边的一半和勾股定理即可解题.
解：（1）∵CD⊥AB， BE⊥AB，
∴CD∥BE,
∵BE=CD,
∴四边形CDBE是矩形,
（2）在Rt△ABC中，
∵∠ABC=30°，AC=2 ，
∴AB=4,（30°角所对直角边是斜边的一半）
∴DE=BC=2（勾股定理）
练习册系列答案
相关题目
