题目内容
【题目】 请将下列证明过程补充完整：
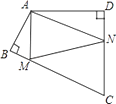
已知：∠1=∠E，∠B=∠D．求证：AB∥CD
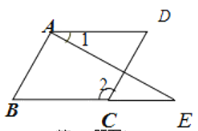
证明：∵ ∠1=∠E（ 已知 ）
∴ ∥ （ ）
∴ ∠D+∠2=180° （ ）
∵ ∠B=∠D（ 已知 ）
∴ ∠B+ ∠2= 180° ( )
∴ AB∥CD （ ）
【答案】∵∠1＝∠E（已知），
∴AD∥BE（内错角相等，两直线平行），
∴∠D＋∠2＝180°（两直线平行，同旁内角互补）；
∵∠B＝∠D（已知），
∴∠B＋∠2＝180°（等量代换）
∴AB∥CD（同旁内角互补，两直线平行）
【解析】
根据∠1＝∠E可判定AD∥BE，可得∠D和∠2为同旁内角互补；结合∠B＝∠D，可推得∠2和∠B也互补，从而判定AB平行于CD．
证明：∵∠1＝∠E（已知），
∴AD∥BE（内错角相等，两直线平行），
∴∠D＋∠2＝180°（两直线平行，同旁内角互补）；
∵∠B＝∠D（已知），
∴∠B＋∠2＝180°，
∴AB∥CD．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
