题目内容
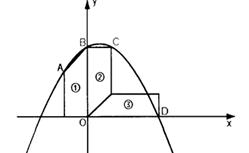
三个全等的直角梯形①、②、③在平面直角坐标系中的位置如图所示,抛物线y=a x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
(1)求梯形的两腰长;
(2)求抛物线的解析式.
解:(1)由图形②、③可知,
垂直于底边的腰为6-4=2,且梯形的一个内角为45°,
所以梯形的另一条腰长为 ;
;
(2)由(1)得点B的坐标是B(0,6),
可设所求的抛物线为y=ax2+bx+6,
把A(-2,4),C(2,6)代入得,
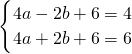
解得
∴抛物线的解析式是y=- x2+
x2+ x+6.
x+6.
分析:(1)由图知:梯形②③的两个内角正好拼成了一个直角,因此这个直角梯形中有一个角为45°,根据梯形的两底差以及45°的内角,即可求得两腰的长;
(2)由(1)求得的梯形的两腰长以及已知的两底的长,可求得A、B、C的坐标,进而可利用待定系数法求得该抛物线的解析式.(A、B、C、D四点中,任取三点即可.)
点评:此题考查了直角梯形的性质、等腰直角三角形的性质、二次函数解析式的确定等知识,难度不大,关键在于对图形的理解.
垂直于底边的腰为6-4=2,且梯形的一个内角为45°,
所以梯形的另一条腰长为
 ;
;(2)由(1)得点B的坐标是B(0,6),
可设所求的抛物线为y=ax2+bx+6,
把A(-2,4),C(2,6)代入得,
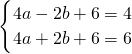
解得

∴抛物线的解析式是y=-
 x2+
x2+ x+6.
x+6.分析:(1)由图知:梯形②③的两个内角正好拼成了一个直角,因此这个直角梯形中有一个角为45°,根据梯形的两底差以及45°的内角,即可求得两腰的长;
(2)由(1)求得的梯形的两腰长以及已知的两底的长,可求得A、B、C的坐标,进而可利用待定系数法求得该抛物线的解析式.(A、B、C、D四点中,任取三点即可.)
点评:此题考查了直角梯形的性质、等腰直角三角形的性质、二次函数解析式的确定等知识,难度不大,关键在于对图形的理解.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
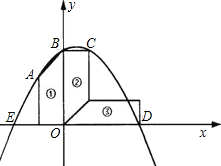 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.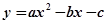 经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6,该抛物线解析式为________________
经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6,该抛物线解析式为________________

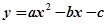 经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6,该抛物线解析式为________________
经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6,该抛物线解析式为________________