题目内容
【题目】 阅读下列材料：我们知道
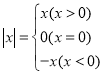
现在我们可以用这个结论来化简含有绝对值的代数式，如化简代数式
时，令
，求得
；令
，求得
（称-1，2分别为
，
的零点值）.在有理数范围内，零点值-1和2可将全体有理数分成不重复且不遗漏的如下3种情况：
①当
时，原式
；
②当
时，原式
；
③当
时，原式
.
综上所述，
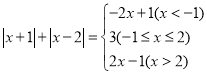
通过以上阅读，请你解决以下问：
(1)分别求出
和
的零点值；
(2)化简代数式
.
【答案】(1)
的零点值为-2，
的零点值是4.(2)当
时,原式
；当-2≤x≤4，原式
；当
时，原式
.
【解析】
（1）根据题中所给材料，求出零点值；（2）将全体实数分成不重复且不遗漏的三种情况解答；
解：
（1）令
，解得
，所以的零点值为-2，令
，解得
，所以
的零点值是4.
（2）当时,原式
；
当-2≤x≤4，原式
；
当时，原式
.
综上所述：
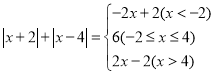
练习册系列答案
计算高手系列答案
相关题目
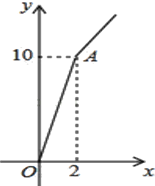
【题目】“十九大”之后，某种子站让利给农民，对价格为a元/千克的种子，如果一次购买2千克以上的，超过2千克部分的种子价格打8折．某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出了函数图象.以下是该科技人员绘制的图象和表格的不完整资料，已知点A的坐标为（2，10）.请你结合表格和图象：
付款金额（元） | a | 7.5 | 10 | 12 | b |
购买量（千克） | 1 | 1.5 | 2 | 2.5 | 3 |
(1)、指出付款金额和购买量哪个变量是函数的自变量x，并写出表中a、b的值；
(2)、求出当x＞2时，y关于x的函数解析式；
(3)、甲农户将8.8元钱全部用于购买该玉米种子，乙农户购买了4165克该玉米种子，分别计算他们的购买量和付款金额.
