Question

【题目】如图，在锐角三角形ABC中，BC＝4，∠ABC＝60°，BD平分∠ABC，交AC于点D，M，N分别是BD，BC上的动点，则CM+MN的最小值是（　　）

A. B. 2C. 2D. 4

Answer 1

【答案】C

【解析】

在BA上截取BE=BN，构造全等三角形△BME≌△BMN，利用三角形的三边的关系确定线段和的最小值．

解：如图，在BA上截取BE=BN，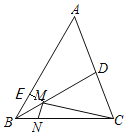

因为∠ABC的平分线交AC于点D，
所以∠EBM=∠NBM，
在△BME与△BMN中，

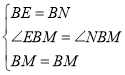
所以△BME≌△BMN（SAS），
所以ME=MN．
所以CM+MN=CM+ME≥CE．
因为CM+MN有最小值．
当CE是点C到直线AB的距离时，即C到直线AB的垂线段时，CE取最小值为：4×sin60°=2

故选：C．