题目内容
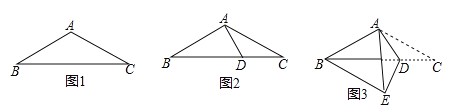
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.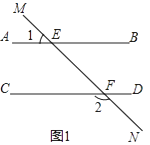
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,PF∥GH,求证:GH⊥EG;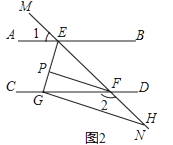
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.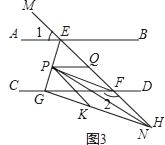
【答案】
(1)解:∵∠1+∠AEF=180°,
∠1+∠2=180°,
∴∠AEF=∠2,
∴AB∥CD.
(2)解:∵AB∥CD,
∴∠AEF+∠EFC=180°;
∵∠AEF与∠EFC的角平分线交于点P,
∴∠PEF+∠PFE=90°,即PF⊥GE;
∵PF∥GH,
∴GH⊥EG
(3)解:∵PF∥GH,
∴∠FPH=∠PHK,而∠PHK=∠HPK,
∴∠FPH=∠KPH(设为α);
∵PQ平分∠EPK,
∴∠KPQ= ![]() =45°+α,
=45°+α,
∴∠HPQ=45°+α﹣α=45°,
即∠HPQ的大小不会发生变化
【解析】掌握对顶角的性质以及平行线的判定定理进行解决实际问题.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目