题目内容
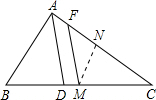
如图，在△ABC中，AB=3，AC=5，点M是BC的中点，AD是∠BAC的平分线，MF∥AD，则FC的长为______．
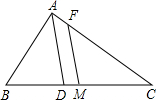
如图，设点N是AC的中点，连接MN，则
MN∥AB，MN=
AB．
∴∠CNM=∠BAC．
∵MF∥AD，
∴∠DAC=∠MFN．
∵AD是∠BAC的平分线，∠CNM=∠MFN+∠FMN，
∴∠MFN=∠FMN．
∴FN=MN=
AB，
∴FC=FN+NC=
AB+
AC=4．
故答案为4．
MN∥AB，MN=
| 1 |
| 2 |
∴∠CNM=∠BAC．
∵MF∥AD，
∴∠DAC=∠MFN．
∵AD是∠BAC的平分线，∠CNM=∠MFN+∠FMN，
∴∠MFN=∠FMN．
∴FN=MN=
| 1 |
| 2 |
∴FC=FN+NC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为4．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
