Question

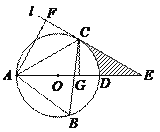
【题目】已知：如图⊙O是以等腰三角形ABC的底边BC为直径的外接圆，BD平分∠ABC交⊙O于D，且BD与OA、AC分别交于点E、F延长BA、CD交于G．

（1）试证明：BF=CG．

（2）线段CD与BF有什么数量关系？为什么？

（3）试比较线段CD与BE的大小关系，并说明理由．

Answer 1

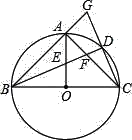
【答案】（1）见解析；（2）线段2CD=BF，理由见解析；（3）见解析.

【解析】

（1）根据圆周角定理以及全等三角形的判定得出△ABF≌△ACG即可求出答案；

（2）利用角平分线的性质以及圆周角定理得出△BDG≌△BDC，进而得出GD=CD，求出，即可得出答案；

（3）利用等腰三角形的性质得出BE=EC，再利用直角三角形边之间大小关系求出即可．

（1）∵⊙O是以等腰三角形ABC的底边BC为直径的外接圆，

∴AB=AC，∠BAC=90°，∠ABD=∠DCA，

∴，

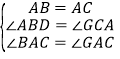∴△ABF≌△ACG，（AAS）

∴BF=CG；

（2）线段2CD=BF，

证明：∵BD平分∠ABC交⊙O于D，

∴∠GBD=∠CBD，

∵BC为直径，

∴∠BDC=90°，

∴，

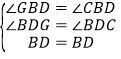∴△BDG≌△BDC，（AAS）

∴GD=CD，

∵BF=CG，

∴，

即，

∴2CD=BF；

（3）连接EC，

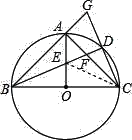
∵△ABC是等腰三角形，AB=AC，

且BO=CO，

∴AO⊥BC（等腰三角形三线合一），

∴BE=EC，

∵∠EDC=90°，在△EDC中所对斜边为EC，

∴EC＞CD（直角三角形中斜边大与直角边长），

∴BE＞CD．