题目内容
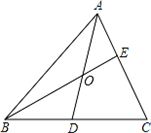
如图,AD和BE把△ABC分成三个三角形和一个四边形,其中△OAE、△OAB、△OBD的面积分别为10、20、16,则四边形ODCE的面积是______.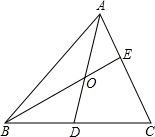

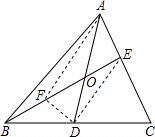
如下图所示:取OB的中点F,连接AF、DF、DE,
易知:S△ABF=S△AFO=
| 1 |
| 2 |
由于S△OAE=10=S△ABF=S△AFO,
由三角形的面积公式可得BF=OF=OE,
所以易知:S△ODE=S△FBD=S△FOD=
| 1 |
| 2 |
设S△DEC=S,则:
S△ABD=S△OAB+S△OBD=20+16=36,
S△ADC=S△OAE+S△ODE+S△DEC=10+8+S=18+S,
S△BDE=S△OBD+S△ODE=16+8=24,
由三角形的面积公式可得:
| SABD |
| SADC |
| BD |
| DC |
| 36 |
| 18+S |
| SBDE |
| SEDC |
| BD |
| DC |
| 24 |
| S |
即:
| 36 |
| 18+S |
| 24 |
| S |
四边形ODCE的面积=36+8=44.
故答案为:44.

练习册系列答案
相关题目

 如图,AD和BE把△ABC分成三个三角形和一个四边形,其中△OAE、△OAB、△OBD的面积分别为10、20、16,则四边形ODCE的面积是
如图,AD和BE把△ABC分成三个三角形和一个四边形,其中△OAE、△OAB、△OBD的面积分别为10、20、16,则四边形ODCE的面积是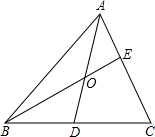 如图,AD和BE把△ABC分成三个三角形和一个四边形,其中△OAE、△OAB、△OBD的面积分别为10、20、16,则四边形ODCE的面积是________.
如图,AD和BE把△ABC分成三个三角形和一个四边形,其中△OAE、△OAB、△OBD的面积分别为10、20、16,则四边形ODCE的面积是________.