题目内容
【题目】如图,四边形![]() 是边长为1的正方形,
是边长为1的正方形,![]() 与
与![]() 轴正半轴的夹角为15°,点
轴正半轴的夹角为15°,点![]() 在抛物线
在抛物线![]() 的图象上,则
的图象上,则![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接OB,过点B作BD⊥x轴于D,根据正方形的性质即可求出OB的长和∠COB的度数,从而求出∠DOB,然后利用锐角三角函数即可求出BD和OD,从而求出点B的坐标,将点B的坐标代入二次函数解析式中即可得出结论.
解:连接OB,过点B作BD⊥x轴于D
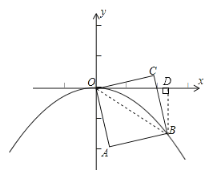
∵四边形![]() 是边长为1的正方形,
是边长为1的正方形,
∴OA=1,OB=![]() OA=
OA=![]() ,∠COB=45°
,∠COB=45°
∵![]() 与
与![]() 轴正半轴的夹角为15°
轴正半轴的夹角为15°
∴∠DOB=∠COB-∠COD=30°
在Rt△OBD中,BD=![]() =
=![]() ,OD=
,OD=![]() ·cos∠DOB=
·cos∠DOB=![]()
∵点B在第四象限
∴点B的坐标为(![]() ,
,![]() )
)
将点B的坐标代入![]() 中,得
中,得
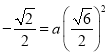
解得:![]()
故选A.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目














