题目内容
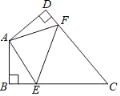
【题目】如图, ![]() 是等边三角形,点
是等边三角形,点 ![]() 在同一条直线上,且
在同一条直线上,且 ![]() .
.
(1)请直接写出图中相似的三角形;
(2)探究 ![]() 之间的关系,并说明理由.
之间的关系,并说明理由.
【答案】
(1)解:△DAE∽△DBA∽△ACE
(2)解:∵△ABC是等边三角形,∴∠ABC=∠ACB=∠BAC=60°.
∴∠D+∠DAB=∠ABC= 60°,∠E+∠CAE=∠ACB=60°.
∵∠DAE=120°,
∴∠DAB+∠CAE=60°.
∴∠D=∠CAE,∠E=∠DAB.
∴△DBA∽△ACE.
∴DB∶AC=AB∶EC.
得DB×EC =AB×AC
∵AB=AC=BC,
∴BC2=DBEC.
【解析】第1小题,图中的相似三角形有:△DAE∽△DBA∽△ACE;第2小题,根据△ABC是等边三角形得到∠ABC=∠ACB=∠BAC=60°.再由已知条件得到
△DBA∽△ACE,结论得证。
【考点精析】根据题目的已知条件,利用等边三角形的性质和相似三角形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;对应角相等,对应边成比例的两个三角形叫做相似三角形.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目