题目内容
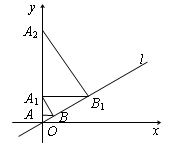
如图,已知直线l: ,过点A(0,1)作y轴的垂线 交直线l于点B,过点B作直线l的垂线交y轴于点A1;过 点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为
,过点A(0,1)作y轴的垂线 交直线l于点B,过点B作直线l的垂线交y轴于点A1;过 点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为
| A.(0,64) | B.(0,128) | C.(0,256) | D.(0,512) |
C.
解析试题分析:∵直线l的解析式为;y=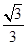 x,
x,
∴l与x轴的夹角为30°,
∵AB∥x轴,
∴∠ABO=30°,
∵OA=1,
∴OB=2,
∴AB=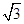 ,
,
∵A1B⊥l,
∴∠ABA1=60°,
∴A1O=4,
∴A1(0,4),
同理可得A2(0,16),
…
∴A4纵坐标为44=256,
∴A4(0,256).
故选C.
考点:一次函数综合题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知k1<0<k2,则函数y=k1x和 的图象大致是( )
的图象大致是( )
A. | B. | C. | D. |
如图,过点Q(0,3.5)的一次函数与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的解析式是( )
A.y= | B.y= | C.y= | D.y=﹣ |
若y=(m-2)x+(m2-4)是正比例函数,则m的取值是( )
| A.2 | B.-2 | C.±2 | D.任意实数 |
根据下图所示程序计算函数值,若输入的 的值为
的值为 ,则输出的函数值为
,则输出的函数值为
A. | B. | C. | D. |
若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(-2,0),则抛物线y=ax2+bx的对称轴为( )
| A.直线x=1 | B.直线x=-2 |
| C.直线x=-1 | D.直线x=-4 |
 (a≠0)在同一直角坐标系中的图像可能是( )
(a≠0)在同一直角坐标系中的图像可能是( )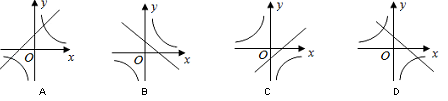
 千米,休息了一段时间,又原路原速返回了
千米,休息了一段时间,又原路原速返回了 千米(
千米( ),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离
),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离 与时间
与时间 的函数关系的大致图象是( ).
的函数关系的大致图象是( ).
 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )