题目内容
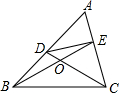 我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.(1)请写出一个你学过的四边形中是等对边四边形的图形的名称;
(2)在△ABC中,如果∠A是锐角,点D,E分别在AB,AC上,且∠DCB=∠EBC=
| 1 | 2 |
分析:(1)等腰梯形,平行四边形等都是等对边四边形;
(2)过B作BF⊥CD交CD延长线于F,过C作CG⊥BE于G,证△CFB≌△BGC,推出BF=CG,求出∠BDF=∠GEC,证△BDF≌△CEG,推出BD=CE即可.
(2)过B作BF⊥CD交CD延长线于F,过C作CG⊥BE于G,证△CFB≌△BGC,推出BF=CG,求出∠BDF=∠GEC,证△BDF≌△CEG,推出BD=CE即可.
解答:解:(1)等腰梯形,如图:AB=DC.

(2)此时存在等对边四边形DBCE,
证明:过B作BF⊥CD交CD延长线于F,过C作CG⊥BE于G,
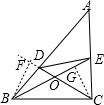
则∠BFC=∠CGB=90°,
∵在△CFB和△BGC中
∴△CFB≌△BGC(AAS),
∴BF=CG,
∵∠BDF=∠ABC+∠DCB=∠ABE+∠EBC+∠DCB=∠ABE+∠A,
∠GEC=∠A+∠ABE,
∴∠BDF=∠GEC,
∵在△BDF和△CEG中
,
∴△BDF≌△CEG(AAS),
∴BD=CE,
即存在等对边四边形DBCE.

(2)此时存在等对边四边形DBCE,
证明:过B作BF⊥CD交CD延长线于F,过C作CG⊥BE于G,

则∠BFC=∠CGB=90°,
∵在△CFB和△BGC中
|
∴△CFB≌△BGC(AAS),
∴BF=CG,
∵∠BDF=∠ABC+∠DCB=∠ABE+∠EBC+∠DCB=∠ABE+∠A,
∠GEC=∠A+∠ABE,
∴∠BDF=∠GEC,
∵在△BDF和△CEG中
|
∴△BDF≌△CEG(AAS),
∴BD=CE,
即存在等对边四边形DBCE.
点评:本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力和理解能力.

练习册系列答案
相关题目
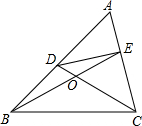 述条件的图形中是否存在等对边四边形,并证明你的结论.
述条件的图形中是否存在等对边四边形,并证明你的结论.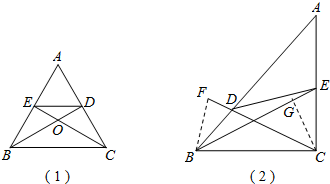
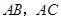 上,设
上,设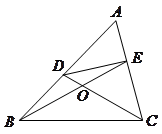
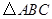 中,如果
中,如果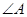 是不等于
是不等于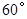 的锐角,点
的锐角,点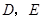 分别在
分别在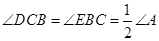 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.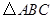 中,点
中,点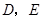 分别在
分别在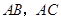 上,设
上,设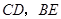 相交于点
相交于点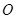 ,若
,若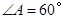 ,
,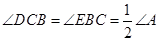 .请你写出图中一个与
.请你写出图中一个与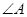 相等的角,并猜想图中哪个四边形是等对边四边形;
相等的角,并猜想图中哪个四边形是等对边四边形;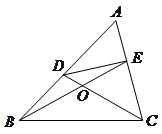
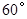 的锐角,点
的锐角,点