题目内容
（2011•桃江县模拟）阅读材料：我们知道，有两条边相等的三角形叫做等腰三角形；类似地，我们定义：至少有一组对边相等的四边形叫做等对边四边形．
（1）如图（1），O是等边△ABC的内心，连接BO、CO并延长分别交AB、AC于点E、D，连接DE，求证：四边形BCDE是等对边四边形；
（2）如图（2），在不等边△ABC中，点D、E分别是边AB、AC上的点，DE≠BC，且满足∠EBC=∠DCB=25°，若四边形BCED是等对边四边形，求∠A的度数．（提示：作BF⊥CD交CD的延长线于F，CG⊥BE于G）
（1）如图（1），O是等边△ABC的内心，连接BO、CO并延长分别交AB、AC于点E、D，连接DE，求证：四边形BCDE是等对边四边形；
（2）如图（2），在不等边△ABC中，点D、E分别是边AB、AC上的点，DE≠BC，且满足∠EBC=∠DCB=25°，若四边形BCED是等对边四边形，求∠A的度数．（提示：作BF⊥CD交CD的延长线于F，CG⊥BE于G）
分析：（1）根据等边三角形性质和内心求出BE=CD=
AB，即可得出答案；
（2）作BF⊥CD交CD的延长线于F，CG⊥BE于G，根据AAS证Rt△BCF≌Rt△CBG，推出BF=CG，证Rt△BDF≌Rt△CEG，推出∠BDF=∠CEG，求出∠BDF=∠DBE+50°，∠CEG=∠A+∠DBE，即可得出答案．
| 1 |
| 2 |
（2）作BF⊥CD交CD的延长线于F，CG⊥BE于G，根据AAS证Rt△BCF≌Rt△CBG，推出BF=CG，证Rt△BDF≌Rt△CEG，推出∠BDF=∠CEG，求出∠BDF=∠DBE+50°，∠CEG=∠A+∠DBE，即可得出答案．
解答：（1）证明：∵O是等边三角形ABC的内心，
∴BD、CE都是三角形ABC的中线，
∴AD=DC=
AC，AE=BE=
AB，AB=AC，
∴BE=CD，
即四边形BCDE是等对边四边形．
（2）解：作BF⊥CD交CD的延长线于F，CG⊥BE于G，
在Rt△BCF与Rt△CBG中
，
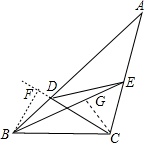
∴Rt△BCF≌Rt△CBG（AAS），
∴BF=CG，
在Rt△BDF与Rt△CEG中，
，
∴Rt△BDF≌Rt△CEG（HL），
∴∠BDF=∠CEG，
∵∠BDF=∠DBE+∠EBC+∠BCD=∠DBE+50°，∠CEG=∠A+∠DBE
∴∠A=50°．
∴BD、CE都是三角形ABC的中线，
∴AD=DC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=CD，
即四边形BCDE是等对边四边形．
（2）解：作BF⊥CD交CD的延长线于F，CG⊥BE于G，
在Rt△BCF与Rt△CBG中
|
∴Rt△BCF≌Rt△CBG（AAS），
∴BF=CG，
在Rt△BDF与Rt△CEG中，
|
∴Rt△BDF≌Rt△CEG（HL），
∴∠BDF=∠CEG，
∵∠BDF=∠DBE+∠EBC+∠BCD=∠DBE+50°，∠CEG=∠A+∠DBE
∴∠A=50°．
点评：本题考查了等边三角形性质和全等三角形的性质和判定的应用，主要考查学生运用性质进行推理的能力，第（2）有一定的难度，对学生提出较高的要求．
练习册系列答案
相关题目
（2011•桃江县模拟）如图，将透明的三角板（其中∠A=90°）置于平行线l1、l2上，则∠α的度数为
（2011•桃江县模拟）如图是我县某地三月份1到10日每天最低气温条形统计图，根据统计图可知，这10天最低气温的众数和中位数分别是
（2011•桃江县模拟）如图，BD是⊙O的直径，A、C是⊙O上的两点，AE⊥CD交CD的延长线于点E，AD平分∠BDE．