题目内容
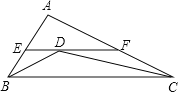
【题目】如图（1）所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止，点Q以2cm/秒的速度沿BC运动到点C时停止．设P、Q同时出发t秒时，△BPQ的面积为ycm2 ． 已知y与t的函数关系图像如图（2）（其中曲线OG为抛物线的一部分，其余各部分均为线段）．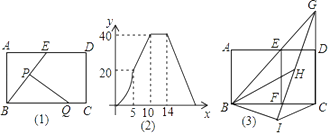
（1）试根据图（2）求0＜t≤5时，△BPQ的面积y关于t的函数解析式；
（2）求出线段BC、BE、ED的长度；
（3）当t为多少秒时，以B、P、Q为顶点的三角形和△ABE相似；
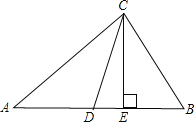
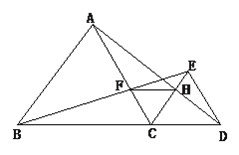
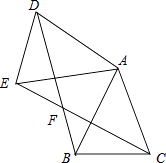
（4）如图（3）过E作EF⊥BC于F，△BEF绕点B按顺时针方向旋转一定角度，如果△BEF中E、F的对应点H、I恰好和射线BE、CD的交点G在一条直线，求此时C、I两点之间的距离．
【答案】
（1）
解：观察图像可知，AD=BC=5×2=10，BE=1×10=10，ED=4×1=4，AE=10﹣4=6
在Rt△ABE中，AB= 
= 
=8，
如图1中，作PM⊥BC于M．
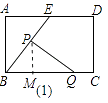
∵△ABE∽△MPB，
∴ 
，
∴ 
= 
，
∴PM= 
t，
当0＜t≤5时，△BPQ的面积y= 
BQPM= 2t t= t2
（2）
解：由（1）可知BC=BE=10，ED=4
（3）
解：①当P在BE上时，
∵BQ=2PB，
∴只有∠BPQ=90°，才有可能B、P、Q为顶点的三角形和△ABE相似，
∴∠BQP=30°，这个显然不可能，
∴当点P在BE上时，不存在△PQB与△ABE相似．
②当点P在ED上时，观察图像可知，不存在△．
③当点P在DC上时，设PC=a，
当 
时，∴ 
= 
，
∴a= 
，
此时t=10+4+（8﹣ ）=14.5，
∴t=14.5s时，△PQB与△ABE相似
（4）
解：如图3中，设EG=m，GH=n，
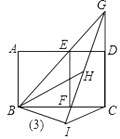
∵DE∥BC，
∴ 
，
∴ 
= 
，
∴m= 
，
在Rt△BIG中，∵BG2=BI2+GI2，
∴（ 
）2=62+（8+n）2，
∴n=﹣8+8 
或﹣8﹣8 （舍弃），
∵∠BIH=∠BCG=90°，
∴B、I、C、G四点共圆，
∴∠BGH=∠BCI，
∵∠GBF=∠HBI，
∴△GBH∽△CBI，
∴ 
，
∴ 
= 
，
∴IC= 
﹣ 
【解析】（1）观察图像可知，AD=BC=5×2=10，BE=1×10=10，ED=4×1=4，AE=10﹣4=6在Rt△ABE中，AB= = =8，如图1中，作PM⊥BC于M．由△ABE∽△MPB，得 ，求出PM，根据△BPQ的面积y= BQPM计算即可问题．（2）观察图像（1）（2），即可解决问题．（3）分三种情形讨论①P在BE上，②P在DE上，③P在CD上，分别求解即可．（4）由∠BIH=∠BCG=90°，推出B、I、C、G四点共圆，推出∠BGH=∠BCI，由△GBH∽△CBI，可得 ，由此只要求出GH即可解决问题．
【考点精析】利用相似三角形的性质和相似三角形的判定对题目进行判断即可得到答案，需要熟知对应角相等，对应边成比例的两个三角形叫做相似三角形；相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）．
