��Ŀ����
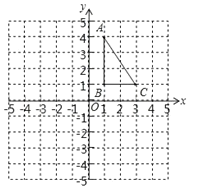
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ����ࣩ����
����ࣩ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() ����
����![]() ���������ϣ�
���������ϣ�
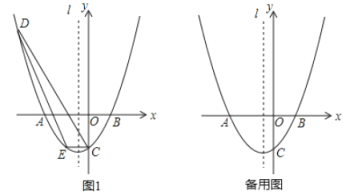
��1����ͼ1��![]() Ϊֱ��
Ϊֱ��![]() �·��������ϵ�һ�㣬����
�·��������ϵ�һ�㣬����![]() ��
��![]() ����
����![]() ��������ʱ����ֱ��
��������ʱ����ֱ��![]() ��ȡһ��
��ȡһ��![]() ����
����![]() ��
��![]() ��Ĵ��ߣ�����Ϊ��
��Ĵ��ߣ�����Ϊ��![]() ������
������![]() ��
��![]() ����
����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��2����������![]() ��
��![]() ��������ƽ�Ƶõ���������
��������ƽ�Ƶõ���������![]() ��
��![]() ����ԭ��
����ԭ��![]() ��
��![]() ��
��![]() �����һ������Ϊ
�����һ������Ϊ![]() ����
����![]() ��������
��������![]() ������һ�㣬��
������һ�㣬��![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() �ܷ��Ϊ�Ե�
�ܷ��Ϊ�Ե�![]() Ϊֱ�Ƕ���ĵ���ֱ�������Σ����ܡ�ֱ��д����
Ϊֱ�Ƕ���ĵ���ֱ�������Σ����ܡ�ֱ��д����![]() �����꣬�����ܣ���˵�����ɣ�
�����꣬�����ܣ���˵�����ɣ�
���𰸡���1��![]() ��2���ܣ�P�������Ϊ��
��2���ܣ�P�������Ϊ�� ��
��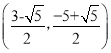 ��
��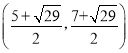 ��
��
��������
(1) ����������¡�C�� D�������꣬���ô���ϵ�������ֱ��CD��ֱ�߷��̣���ͼ1�У�����E��EG //y�ύֱ��CD��G����E (m,![]() +2m-3)����G (m,-2m-3)��GE=-
+2m-3)����G (m,-2m-3)��GE=-![]() -4m������S��EDC=
-4m������S��EDC=![]() ��EG��|DX|=
��EG��|DX|=![]() (-
(-![]() -4m) ��4=-2
-4m) ��4=-2![]() +8����֪m=-2ʱ����DEC��������ʱE(-2, -3) ����֤��Rt��EHM��Rt��BON���ɽ�����⣻
+8����֪m=-2ʱ����DEC��������ʱE(-2, -3) ����֤��Rt��EHM��Rt��BON���ɽ�����⣻
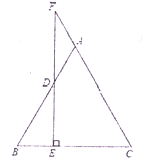
��2���������.��ͼ2��.��P M��x����M��P N�ͶԳ���|��N���Գ���l|��0A��K������PMF�ա�PNQ���Ƴ�PM=PN���Ƴ���P�ڡ�MKN�Ľ�ƽ�����ϣ�ֻҪ���ֱ��KP�Ľ���ʽ�����������鼴�����P��P�����꣬ͬ������P�� P4�����꣮
�⣺��1��������A(1,0)��B(-3,0)��C(0,-3)��D(-4,5)��
��ֱ��CD�Ľ���ʽΪy= kx+b,����
b=-3��-4k+b=5 ��k=-2��b=-3
��ֱ��CD�Ľ���ʽΪy=-2x-3
��ͼ1�У�����E��EG��y�ύֱ��CD��G����E(m,![]() +2m-3)����G(m,-2m-3)
+2m-3)����G(m,-2m-3)
��GE=-m-4m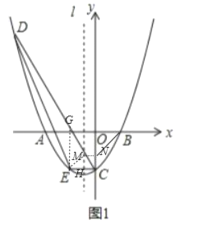
��S��EDC=![]() ��EG��|DX|=
��EG��|DX|=![]() (-
(-![]() -4m) ��4=-2
-4m) ��4=-2![]() +8��
+8��
��-2��0����m=-2ʱ����DEC��������ʱE(-2,-3)��
��C(0,-3)��
��EC��AB����CE���Գ�����H����B(1,0)��
��EH=OB=1��
��EM=BN��
��Rt��EHM��Rt��BON��
��MH=ON=![]() OC=
OC=![]()
��EM=BN=![]() ��
��
��EM+MN+MB=![]()
��2��������������ĵ㣬��ͼ2����PM��x����M��PN�ͶԳ���l��N���Գ���l��OA��K��
��PQ=PF����QPF=90�㣬��NQP =��MFP ���ɵá�PMF�ա�PNQ
��PM=PN�����P�ڡ�MKN�Ľ�ƽ�����ϣ�
��ֱ��KP��(-1,0)����x���45��ǣ����������������ޣ�
��ֱ��KP�Ľ���ʽΪy=-x-1��
������������ƽ���� 3����λ��
��������y�Ľ���ʽΪy=x-4x��
��P ��������y��ֱ��KP �Ľ���
��![]()
���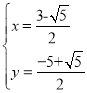 ��
��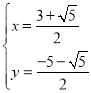
��P ��P
��P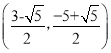

ͬ����֪��ֱ��y=x+1�������ߵĽ���P3��P4����������
��![]()
���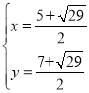 ��
��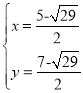
��P3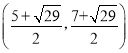
P4
�������������������ĵ�P����Ϊ��
 ��
��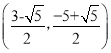 ��
��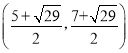 ��
��

 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�