题目内容
观察探究:小明同学非常细心,火柴盒在桌面上倒下,便启迪他得到很多发现.如图,火柴盒的一个侧面ABCD逆时针方向倒下后到AB′C′D′的位置,连接CC′.设AB=b,BC=a,AC=c.

(1)他在学习了因式分解后,意外地发现,代数式a2-b2表示了图中一个长方形的面积,请你把这个长方形画完整,并把它指出来;
(2)学过勾股定理之后,他又惊奇地发现,利用四边形BCC′D′的面积可以得到证明勾股定理的新方法,请你利用这个四边形的面积证明勾股定理:a2+b2=c2.
分析:(1)根据题意作出长为(a+b),宽为(a-b)的长方形图形;
(2)四边形BCC′D′的面积从大的一方面来说属于直角梯形,可利用直角梯形的面积公式进行表示从组成来看,由三个直角三角形组成.应利用三角形的面积公式来进行表示.
(2)四边形BCC′D′的面积从大的一方面来说属于直角梯形,可利用直角梯形的面积公式进行表示从组成来看,由三个直角三角形组成.应利用三角形的面积公式来进行表示.
解答: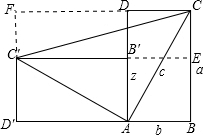 解:(1)延长C′B′交BC于E,再延长D′C′交CD的延长线于点F,
解:(1)延长C′B′交BC于E,再延长D′C′交CD的延长线于点F,
则长方形C′ECF即为所求.
(2)依题意,图中的四边形BCC′D′为直角梯形,△CC′A为等腰直角三角形,
Rt△ABC和Rt△C′D′A的形状和大小完全一样
设梯形BCC′D′的面积为S,则S=
(a+b)(a+b)=
(a2+b2)+ab
又∵S=SRt△CC'A+2SRt△ABC=
c2+2×
ab=
c2+ab
∴
(a2+b2)+ab=
c2+ab.
因此,a2+b2=c2
 解:(1)延长C′B′交BC于E,再延长D′C′交CD的延长线于点F,
解:(1)延长C′B′交BC于E,再延长D′C′交CD的延长线于点F,则长方形C′ECF即为所求.
(2)依题意,图中的四边形BCC′D′为直角梯形,△CC′A为等腰直角三角形,
Rt△ABC和Rt△C′D′A的形状和大小完全一样
设梯形BCC′D′的面积为S,则S=
| 1 |
| 2 |
| 1 |
| 2 |
又∵S=SRt△CC'A+2SRt△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
因此,a2+b2=c2
点评:本题考查了勾股定理的证明,需注意:组成的图形的面积有两种表示方法:大的面积的表示方法和各个组成部分的面积的和.

练习册系列答案
相关题目
 (2013•广阳区一模)九年级数学兴趣小组近期开展了对运动型问题的探究.小明同学提供了一个这样的背景:如图,在?ABCD中,AB=AC=10cm,sin∠ACB=
(2013•广阳区一模)九年级数学兴趣小组近期开展了对运动型问题的探究.小明同学提供了一个这样的背景:如图,在?ABCD中,AB=AC=10cm,sin∠ACB=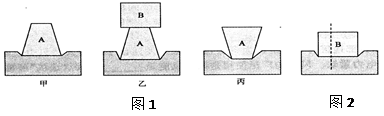
 ,动点O从A出发以1cm/s的速度沿AC方向向点C匀速运动,同时线段EF从与线段CB重合的位置出发以1cm/s的速度沿BA方向向点C匀速运动.在运动过程中,EF交AC于点G,连接OE、OF.设运动时间为ts(0<t<10),请你解决以下问题:
,动点O从A出发以1cm/s的速度沿AC方向向点C匀速运动,同时线段EF从与线段CB重合的位置出发以1cm/s的速度沿BA方向向点C匀速运动.在运动过程中,EF交AC于点G,连接OE、OF.设运动时间为ts(0<t<10),请你解决以下问题: