题目内容
【题目】如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行几米?
【答案】解:如图,设大树高为AB=10m,小树高为CD=4m,过C点作CE⊥AB于E,则四边形EBDC是矩形,连接AC,
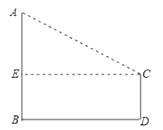
∴EB=4m,EC=8m,AE=AB﹣EB=10﹣4=6m,
在Rt△AEC中,AC= ![]() =10m,
=10m,
答:一只鸟从一颗树的树梢飞到另一颗树的树梢,小鸟至少飞行10m.
【解析】根据题意抽象出几何图形,设大树高为AB=10m,小树高为CD=4m,过C点作CE⊥AB于E,根据矩形的判定得出四边形EBDC是矩形 ,根据矩形的性质得出EB=4m,EC=8m ,从而得出AE的长,在Rt△AEC中,利用勾股定理算出AC的长,即知道了小鸟飞行的最短距离。

练习册系列答案
相关题目