题目内容
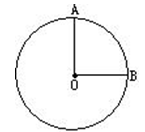
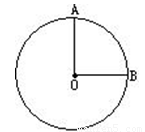
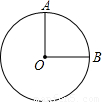
如图，半径为2的圆形纸片，沿半径OA、OB裁成1：3两部分，用得到的扇形围成圆锥的侧面，则圆锥的底面半径分别为 ．
【答案】分析：利用勾股定理，弧长公式，圆的周长公式求解．
解答：
解：如图，分两种情况，
①设扇形S2做成圆锥的底面半径为R2，
由题意知：扇形S2的圆心角为270度，
则它的弧长=
=2πR2，R2=
；
②设扇形S1做成圆锥的底面半径为R1，
由题意知：扇形S1的圆心角为90度，
则它的弧长=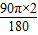
=2πR1，R1=
．
故答案为
或
．
点评：本题利用了勾股定理，弧长公式，圆的周长公式求解．在中考中作为必考点之一经常出现．
解答：
解：如图，分两种情况，①设扇形S2做成圆锥的底面半径为R2，
由题意知：扇形S2的圆心角为270度，
则它的弧长=
=2πR2，R2=；②设扇形S1做成圆锥的底面半径为R1，
由题意知：扇形S1的圆心角为90度，
则它的弧长=
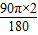=2πR1，R1=．故答案为
或．点评：本题利用了勾股定理，弧长公式，圆的周长公式求解．在中考中作为必考点之一经常出现．
练习册系列答案
相关题目
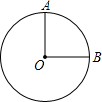如图，半径为2的圆形纸片，沿半径OA、OB裁成1：3两部分，用得到的扇形围成圆锥的侧面，则圆锥的底面半径分别为
