题目内容
【题目】如图,AB与CD相交于O , OE平分∠AOC , OF⊥AB于O , OG⊥OE于O , 若∠BOD=40°,求∠AOE和∠FOG的度数.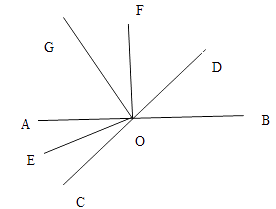
【答案】解:∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=40°,
∵OE平分∠AOC,
∴∠AOE= ![]() ∠AOC=20°,
∠AOC=20°,
∵OF⊥AB,OG⊥OE,
∴∠AOF=∠EOG=90°,
即∠AOG与∠FOG互余,∠AOG与∠AOE互余,
∴∠FOG=∠AOE=20°
【解析】根据对顶角相等可得∠AOC=∠BOD,根据OE平分∠AOC可得∠AOE= ![]() ∠AOC,再由OF⊥AB,OG⊥OE,可得∠AOF=∠EOG,即∠AOG与∠FOG互余,∠AOG与∠AOE互余,那么∠FOG=∠AOE。
∠AOC,再由OF⊥AB,OG⊥OE,可得∠AOF=∠EOG,即∠AOG与∠FOG互余,∠AOG与∠AOE互余,那么∠FOG=∠AOE。

练习册系列答案
相关题目