题目内容
【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM. 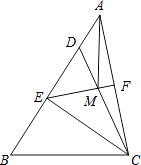
(1)求证:EF= ![]() AC.
AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
【答案】
(1)证明:∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF= ![]() AC
AC
(2)解:∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM
【解析】(1)根据等腰三角形三线合一的性质可得CE⊥BD,再根据直角三角形斜边上的中线等于斜边的一半可得EF= ![]() AC;(2)判断出△AEC是等腰直角三角形,根据等腰直角三角形的性质可得EF垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM,然后求出CD=AM+DM,再等量代换即可得解.
AC;(2)判断出△AEC是等腰直角三角形,根据等腰直角三角形的性质可得EF垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM,然后求出CD=AM+DM,再等量代换即可得解.
【考点精析】关于本题考查的等腰直角三角形和直角三角形斜边上的中线,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形斜边上的中线等于斜边的一半才能得出正确答案.

练习册系列答案
相关题目