题目内容
【题目】如图为住宅区内的两幢楼，它们的高AB=CD=30m，两楼之间的距离AC=24m，现需了解甲楼对乙楼的采光的影响情况，当太阳光与水平线的夹角为30°时，求甲楼的影子在乙楼上有多高？（精确到0.1m，
≈1.41，
≈1.73）？
【答案】16.2m.
【解析】
通过投影的知识结合题意构造直角三角形Rt△BEF，根据含
角的直角三角形的性质及勾股定理即可求出甲楼的影子在乙楼上有多高.
设甲楼的影子在乙楼上的最高点为E，作EF⊥AB于F，
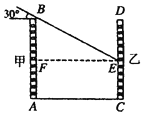
在Rt△BFE中，
∵∠BFE=90°，∠BEF=30°，
∴BF=
BE，
根据勾股定理，得BF2+EF2=BE2，
∴BF2+242=4BF2，
即BF=8
≈13.8m，
∴CE=AF=AB-BF=16.2（m）．
练习册系列答案
相关题目
