题目内容
【题目】已知正方形ABCD,一等腰直角三角板的一个锐角顶点与A重合,将此三角板绕A点旋转时,两边分别交直线BC、CD于M、N.
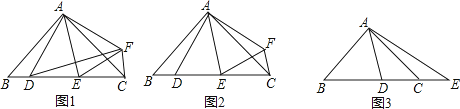
(1)当M、N分别在边BC、CD上时(如图1),求证:BM+DN=MN;
(2)当M、N分别在边BC、CD所在的直线上时(如图2),线段BM、DN、MN之间又有怎样的数量关系,请直接写出结论 ;(不用证明)
(3)当M、N分别在边BC、CD所在的直线上时(如图3),线段BM、DN、MN之间又有怎样的数量关系,请写出结论并写出证明过程.

【答案】(1)证明见解析;(2)BM﹣DN=MN;(3)DN﹣BM=MN;证明见解析;
【解析】
(1)延长CB到G使BG=DN,由AB=AD,GB=DN,∠AGB=∠ADN=90°,可证明△AGB≌△AND,进而可知AG=AN,∠GAB=∠DAN,由∠MAN=45°,BAD=90°
可知∠GAM=45°,进而证明△AMN≌△AMG,根据MN=GM=BM+GB=MB+DN即可得答案.(2)BM﹣DN=MN;(3)在ND上截取DG=BM,可证明△ADG≌△ABM,进而可知AG=AM,∠MAB=∠DAG, 根据∠MAN=45°,∠BAD=90°,可证明△AMG为等腰直角三角形,可知AN为MG的垂直平分线,进而可知NM=NG,即可证明DN﹣BM=MN.
(1)延长CB到G使BG=DN,
∵AB=AD,GB=DN,∠AGB=∠ADN=90°,
∴△AGB≌△AND,
∴AG=AN ,∠GAB=∠DAN,
∵∠MAN=45°,∠BAD=90°,
∴∠GAM=∠GAB+∠BAM=∠DAN+∠BAM=45°,
∴∠GAM=∠NAM,而AM是公共边,
∴△AMN≌△AMG,
∴MN=GM=BM+GB=MB+DN;
(2)BM﹣DN=MN;
(3)DN﹣BM=MN.如图3,
在ND上截取DG=BM,
∵AD=AB,∠ABM=∠ADN=90°,
∴△ADG≌△ABM,
∴AG=AM,∠MAB=∠DAG,
∵∠MAN=45°,∠BAD=90°,
∴∠MAG=90°,△AMG为等腰直角三角形,
∴AN垂直MG,
∴AN为MG垂直平分线,
所以NM=NG.
∴DN﹣BM=MN.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答为得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
组别 | 分数段 | 频数(人) | 频率 |
1 | 50≤x<60 | 30 | 0.1 |
2 | 60≤x<70 | 45 | 0.15 |
3 | 70≤x<80 | 60 | n |
4 | 80≤x<90 | m | 0.4 |
5 | 90≤x<100 | 45 | 0.15 |
请根据以图表信息,解答下列问题: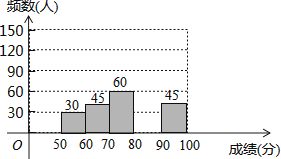
(1)表中m= , n=;
(2)补全频数分布直方图;
(3)全体参赛选手成绩的中位数落在第几组;
(4)若得分在80分以上(含80分)的选手可获奖,记者从所有参赛选手中随机采访1人,求这名选手恰好是获奖者的概率.