题目内容
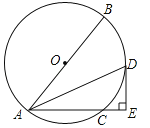
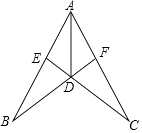
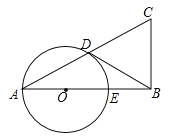
【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:ACAD=ABAE;
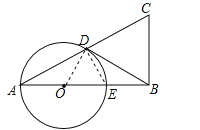
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
【答案】(1)证明见试题解析;(2)4.
【解析】
试题分析:(1)连接DE,根据圆周角定理求得∠ADE=90°,得出∠ADE=∠ABC,进而证得△ADE∽△ABC,根据相似三角形对应边成比例即可求得结论;
(2)连接OD,根据切线的性质求得OD⊥BD,在RT△OBD中,根据已知求得∠OBD=30°,进而求得∠BAC=30°,根据30°的直角三角形的性质即可求得AC的长.
试题解析:(1)连接DE,∵AE是直径,∴∠ADE=90°,∴∠ADE=∠ABC,∵∠DAE=∠BAC,∴△ADE∽△ABC,∴![]() ,∴ACAD=ABAE;
,∴ACAD=ABAE;
(2)解:连接OD,∵BD是⊙O的切线,∴OD⊥BD,在RT△OBD中,OE=BE=OD,∴OB=2OD,∴∠OBD=30°,同理∠BAC=30°,在RT△ABC中,AC=2BC=2×2=4.

练习册系列答案
相关题目
【题目】2018年国家将扩大公共场所免费上网范围,某小区响应号召调查小区居民上网费用情况,随机抽查了30户家庭的月上网费用,结果如表
月网费(元) | 50 | 100 | 150 |
户数(人) | 15 | 12 | 3 |
则关于这30户家庭的月上网费用,中位数是_____.