题目内容
【题目】阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).

(1)求步道的宽.
(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2, 且区域丙为正方形,求塑胶跑道的总面积.
【答案】(1)3.6m (2)199m2
【解析】
(1)步道宽度为a, 则正方形休闲广场的边长为7a, 根据两条步道总面积等于休闲广场面积列方程求解即可.其中注意两条步道总面积要减去重叠部分的小正方形面积.
(2)根据空地的长度和宽度,道路和塑胶的宽度以及丙的边长,计算出甲、乙区域长之差,因两区域的宽度相等,根据面积之差等于长度之差乘以宽度,求得宽度,即正方形丙的边长,塑胶跑道的总面积等于总长度乘以塑胶宽度,总长度等于空地长宽之和加丙的一边长,再减去有两次重复相加的塑胶宽度.
(1)解:由题意,得100a+80a-a2=(7a)2 ,
化简,得a2=3.6a,
∵a>0,
∴a=3.6.
答:步道的宽为3.6 m.
(2)解:如图,
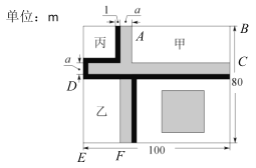
由题意,得AB-DE=100-80+1=21(m),
∴BC=EF=![]() =21(m).
=21(m).
∴塑胶跑道的总面积为1×(100+80+21-2)=199(m2).

【题目】根据下表,回答问题:
x | … | -2 | -1 | 0 | 1 | 2 | … |
-2x+5 | … | 9 | 7 | 5 | 3 | a | … |
2x+8 | … | 4 | 6 | 8 | 10 | b | … |
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.