题目内容
已知反比例函数 ,当
,当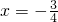 时,y=-4,若一次函数y=mx-2的图象与反比例函数
时,y=-4,若一次函数y=mx-2的图象与反比例函数 的图象有交点,则m的取值范围是
的图象有交点,则m的取值范围是
- A.
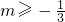 且m≠0
且m≠0 - B.m>
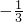
- C.
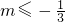 且m≠0
且m≠0 - D.无法确定
A
分析:先将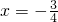 时,y=-4,代入反比例函数
时,y=-4,代入反比例函数 ,求出解析式,再根据函数的图象有交点,用一元二次方程根的判别式可解.
,求出解析式,再根据函数的图象有交点,用一元二次方程根的判别式可解.
解答:当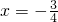 时,y=-4,代入反比例函数
时,y=-4,代入反比例函数 ,
,
则有k=3,
故反比例函数为y=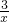 .
.
由联立方程组 ,
,
有mx-2=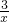 ,即mx2-2x-3=0.
,即mx2-2x-3=0.
要使两个函数的图象有交点,须使方程mx2-2x-3=0有实数根.
∴△=22+12m=4+12m≥0,且m≠0
解得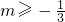 ,且m≠0.
,且m≠0.
故选A.
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.
分析:先将
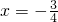 时,y=-4,代入反比例函数
时,y=-4,代入反比例函数 ,求出解析式,再根据函数的图象有交点,用一元二次方程根的判别式可解.
,求出解析式,再根据函数的图象有交点,用一元二次方程根的判别式可解.解答:当
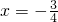 时,y=-4,代入反比例函数
时,y=-4,代入反比例函数 ,
,则有k=3,
故反比例函数为y=
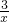 .
.由联立方程组
 ,
,有mx-2=
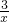 ,即mx2-2x-3=0.
,即mx2-2x-3=0.要使两个函数的图象有交点,须使方程mx2-2x-3=0有实数根.
∴△=22+12m=4+12m≥0,且m≠0
解得
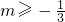 ,且m≠0.
,且m≠0.故选A.
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
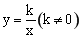


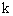
 ,当
,当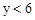 时,x的取值范围是
时,x的取值范围是
 ,当
,当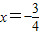 时,y=-4,若一次函数y=mx-2的图象与反比例函数
时,y=-4,若一次函数y=mx-2的图象与反比例函数 的图象有交点,则m的取值范围是( )
的图象有交点,则m的取值范围是( )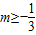 且m≠0
且m≠0
 且m≠0
且m≠0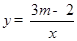 ,当
,当 时,其图象的两个分支在第一、三象限内;当
时,其图象的两个分支在第一、三象限内;当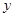 随
随 的增大而增大;
的增大而增大;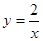 ,当
,当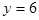 时,
时,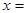 _________
_________