Question

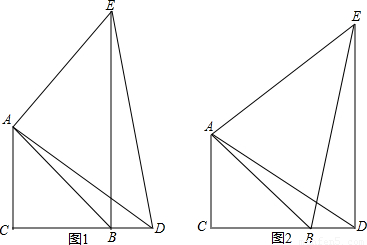
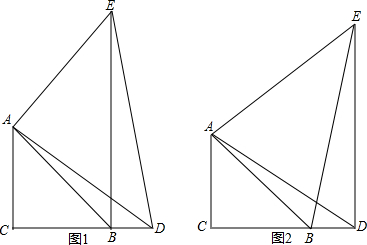
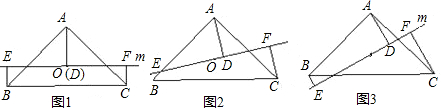
点D为等腰直角三角形ACB的直角边CB的延长线上一点，∠C=90°，连接AD，
（1）如图1，AE⊥AD于A，且AE=AD，连接BE．求证：BE⊥BC；
（2）如图2，AE⊥AB，DE⊥BC交AE于点E，连接EC，BE，求证：．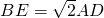

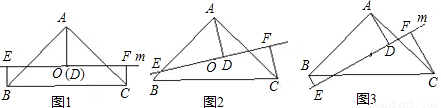
Answer 1

证明：（1）过E作EF⊥CA的延长线于F，
可证△AFE≌△DCA，
∴EF=AC=BC，
∴四边形CBEF为平行四边形，
∴∠CBE=90°，
∴BE⊥BC；

（2）过A作AF⊥DE于F，
可证四边形ACDF为矩形，△AFE为等腰直角三角形，
则△ACD∽△BAE，
．
∴．
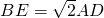分析：（1）作EF⊥CA的延长线于F，证出△AFE≌△ACD，得到EF=AC=BC，根据∠CAF=90°证出四边形CBEF为矩形，从而得出BE⊥BC．
（2）过A作AF⊥DE于F，得到△ACD∽△BAE，然后根据等腰三角形的性质解答即可．
点评：此题考查了等腰三角形的性质，作出辅助线，构造直角三角形，根据直角三角形的性质证明三角形全等是解题的关键．